Brandt semigroup
Encyclopedia
In mathematics, Brandt semigroup
s are completely 0-simple inverse semigroup
s. In other words, they are semigroups without proper ideal and which are also inverse semigroups. They are build in the same way that completely 0-simple semigroups:
Let G be a group
and
be non-empty sets. We define the matrix 
of dimension 
with entry in 
Then, it can be shown that every 0-simple semigroup are of the form
with the operation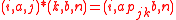 
.
As Brandt semigroup are also inverse semigroup, it changes a bit the configuration of the construction. In fact, instead of 2 difference set I ans J, it is shown in Howie (1995) that to respect the inverse condition, the construction has to be with a unique set I.
So, the Brandt semigroup has the form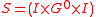
with the operation 
.
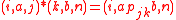Moreover, the matrix is diagonal with only the identity e in its diagonal.
2) There are equivalent way to define the Brandt semigroup. Here is another one:
ac=bc≠0 or ca=cb≠0 ⇒ a=b
ab≠0 and bc≠0 ⇒ abc≠0
If a ≠ 0 then there is unique x,y,z for which xa = a, ay = a, za = y.
For all idempotents e and f nonzero, eSf ≠ 0
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s are completely 0-simple inverse semigroup
Inverse semigroup
In mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
s. In other words, they are semigroups without proper ideal and which are also inverse semigroups. They are build in the same way that completely 0-simple semigroups:
Let G be a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and
be non-empty sets. We define the matrix of dimension with entry in Then, it can be shown that every 0-simple semigroup are of the form
with the operation 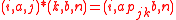.As Brandt semigroup are also inverse semigroup, it changes a bit the configuration of the construction. In fact, instead of 2 difference set I ans J, it is shown in Howie (1995) that to respect the inverse condition, the construction has to be with a unique set I.
So, the Brandt semigroup has the form
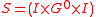with the operation 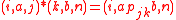.Moreover, the matrix is diagonal with only the identity e in its diagonal.
Remarques
1) The idempotents have the form (i,e,i) where e is the identity of G2) There are equivalent way to define the Brandt semigroup. Here is another one:
ac=bc≠0 or ca=cb≠0 ⇒ a=b
ab≠0 and bc≠0 ⇒ abc≠0
If a ≠ 0 then there is unique x,y,z for which xa = a, ay = a, za = y.
For all idempotents e and f nonzero, eSf ≠ 0