Bonferroni correction
Encyclopedia
In statistics
, the Bonferroni correction is a method used to counteract the problem of multiple comparisons
. It was developed and introduced by Italian
mathematician
Carlo Emilio Bonferroni
. The correction is based on the idea that if an experimenter is testing n dependent or independent hypotheses
on a set of data, then one way of maintaining the familywise error rate
is to test each individual hypothesis at a statistical significance
level of 1/n times what it would be if only one hypothesis were tested. So, if it is desired that the significance level for the whole family of tests should be (at most) α, then the Bonferroni correction would be to test each of the individual tests at a significance level of α/n. Statistically significant simply means that a given result is unlikely to have occurred by chance assuming the null hypothesis
is actually correct (i.e., no difference among groups, no effect of treatment, no relation among variables).
The Bonferroni correction is derived by observing Boole's inequality
. If n tests are performed, each of them significant with probability β, (where β is unknown) then the probability that at least one of them comes out significant is (by Boole's inequality) ≤ nβ. Our intention is for this probability to equal α, the significance level for the entire series of tests. By solving for β, we get β = α/n. This result does not require that the tests be independent.
test procedure (i.e. more powerful regardless of the values of the unobservable parameters) is the Holm–Bonferroni method. However, current methods for obtaining confidence intervals for the Holm-Bonferroni method do not guarantee confidence intervals that are contained within those obtained using the Bonferroni correction. A less restrictive criterion that does not control the familywise error rate is the approximate false discovery rate which does not require ordering the p-values, then using different criteria for each test.
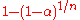
This correction is often confused with the Bonferroni correction. The Šidák correction is derived by assuming that the individual tests are independent. Let the significance threshold for each test be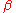
; then the probability that at least one of the tests is significant under this threshold is (1 - the probability that none of them are significant). Since it is assumed that they are independent, the probability that all of them are not significant is the product of the probabilities that each of them are not significant, or 
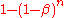. Our intention is for this probability to equal 
, the significance level for the entire series of tests. By solving for 
, we obtain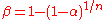 
.
For example, to test two independent hypotheses on the same data at 0.05 significance level, instead of using a p value
threshold of 0.05, one would use a stricter threshold equal to
. Notably one can derive valid confidence intervals matching the test decision using the Šidák correction by using 100(1 − α1/n)% confidence intervals.
The Bonferroni correction is a safeguard against multiple tests of statistical significance on the same data falsely giving the appearance of significance, as 1 out of every 20 hypothesis-tests is expected to be significant at the α = 0.05 level purely due to chance. Furthermore, the probability of getting a significant result with n tests at this level of significance is 1 − 0.95n (1 − probability of not getting a significant result with n tests).
The Šidák correction gives a stronger bound than the Bonferroni correction, because, for
, 
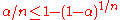. But the Šidák correction requires the additional condition of independence. Previously, because the Šidák correction requires fractional powers (i.e. roots), the computationally simpler Bonferroni correction was often preferred instead. Now, inasmuch as computing fractional powers is trivial, preference of the Bonferroni method is due in part to tradition or unfamiliarity with the Šidák method. Additionally, the results of the two methods are highly similar for conventional significance levels (between .01 and .10).
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Bonferroni correction is a method used to counteract the problem of multiple comparisons
Multiple comparisons
In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
. It was developed and introduced by Italian
Italian people
The Italian people are an ethnic group that share a common Italian culture, ancestry and speak the Italian language as a mother tongue. Within Italy, Italians are defined by citizenship, regardless of ancestry or country of residence , and are distinguished from people...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Carlo Emilio Bonferroni
Carlo Emilio Bonferroni
Carlo Emilio Bonferroni was an Italian mathematician who worked on probability theory. Carlo Emilio Bonferroni was born in Bergamo on 28 January 1892 and died on 18 August 1960 in Firenze . He studied in Torino , held a post as assistant professor at the Turin Polytechnic, and in 1923 took up the...
. The correction is based on the idea that if an experimenter is testing n dependent or independent hypotheses
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
on a set of data, then one way of maintaining the familywise error rate
Familywise error rate
In statistics, familywise error rate is the probability of making one or more false discoveries, or type I errors among all the hypotheses when performing multiple pairwise tests.-Classification of m hypothesis tests:...
is to test each individual hypothesis at a statistical significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
level of 1/n times what it would be if only one hypothesis were tested. So, if it is desired that the significance level for the whole family of tests should be (at most) α, then the Bonferroni correction would be to test each of the individual tests at a significance level of α/n. Statistically significant simply means that a given result is unlikely to have occurred by chance assuming the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
is actually correct (i.e., no difference among groups, no effect of treatment, no relation among variables).
The Bonferroni correction is derived by observing Boole's inequality
Boole's inequality
In probability theory, Boole's inequality, also known as the union bound, says that for any finite or countable set of events, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events...
. If n tests are performed, each of them significant with probability β, (where β is unknown) then the probability that at least one of them comes out significant is (by Boole's inequality) ≤ nβ. Our intention is for this probability to equal α, the significance level for the entire series of tests. By solving for β, we get β = α/n. This result does not require that the tests be independent.
Criticisms
While helpful when used correctly, concerns have been expressed about possible misuse and misunderstanding of Bonferroni correction (see, e.g., Perneger, 1998). First, Bonferroni correction controls the probability of false positives only. The correction ordinarily comes at the cost of increasing the probability of producing false negatives, aka reduced "power". Second, in certain situations where one wants to retain, not reject, the null hypothesis, then Bonferroni correction is non-conservative.Holm-Bonferroni method
A uniformly more powerfulStatistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
test procedure (i.e. more powerful regardless of the values of the unobservable parameters) is the Holm–Bonferroni method. However, current methods for obtaining confidence intervals for the Holm-Bonferroni method do not guarantee confidence intervals that are contained within those obtained using the Bonferroni correction. A less restrictive criterion that does not control the familywise error rate is the approximate false discovery rate which does not require ordering the p-values, then using different criteria for each test.
Šidák correction
A related correction, called the Šidák correction (or Dunn-Šidák correction) that is often used is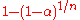This correction is often confused with the Bonferroni correction. The Šidák correction is derived by assuming that the individual tests are independent. Let the significance threshold for each test be
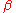; then the probability that at least one of the tests is significant under this threshold is (1 - the probability that none of them are significant). Since it is assumed that they are independent, the probability that all of them are not significant is the product of the probabilities that each of them are not significant, or 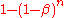. Our intention is for this probability to equal , the significance level for the entire series of tests. By solving for , we obtain 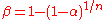.For example, to test two independent hypotheses on the same data at 0.05 significance level, instead of using a p value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
threshold of 0.05, one would use a stricter threshold equal to
. Notably one can derive valid confidence intervals matching the test decision using the Šidák correction by using 100(1 − α1/n)% confidence intervals.The Bonferroni correction is a safeguard against multiple tests of statistical significance on the same data falsely giving the appearance of significance, as 1 out of every 20 hypothesis-tests is expected to be significant at the α = 0.05 level purely due to chance. Furthermore, the probability of getting a significant result with n tests at this level of significance is 1 − 0.95n (1 − probability of not getting a significant result with n tests).
The Šidák correction gives a stronger bound than the Bonferroni correction, because, for
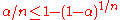, . But the Šidák correction requires the additional condition of independence. Previously, because the Šidák correction requires fractional powers (i.e. roots), the computationally simpler Bonferroni correction was often preferred instead. Now, inasmuch as computing fractional powers is trivial, preference of the Bonferroni method is due in part to tradition or unfamiliarity with the Šidák method. Additionally, the results of the two methods are highly similar for conventional significance levels (between .01 and .10).Dunnett's correction
Dunnett (1955, 1966; not to be confused with Dunn) described an alternative alpha error adjustment when k groups are compared to the same control group. This method is less conservative than the Bonferroni adjustment.See also
- Bonferroni inequalities
- Holm–Bonferroni method
- Multiple testing