
Bollobás–Riordan polynomial
Encyclopedia
The Bollobás–Riordan polynomial can mean a 3-variable polynomial invariant of graphs on orientable surfaces, or a more general 4-variable invariant of ribbon graphs, generalizing the Tutte polynomial
. These polynomials were discovered by .
The 3-variable Bollobás–Riordan polynomial is given by
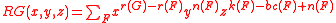
where
Tutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
. These polynomials were discovered by .
The 3-variable Bollobás–Riordan polynomial is given by
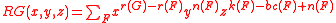
where
- v(G) is the number of vertices of G;
- e(G) is the number of its edges of G;
- k(G) is the number of components of G;
- r(G) is the rank of G such that r(G) = v(G) − k(G);
- n(G) is the nullity of such that n(G) = e(G) − r(G);
- bc(G) is the number of connected components of the boundary of G;

