Block Wiedemann algorithm
Encyclopedia
The block Wiedemann algorithm for computing kernel vectors of a matrix over a finite field is a generalisation of an algorithm due to Don Coppersmith
.
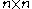square matrix over some finite field F, let 
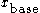be a random vector of length n, and let 
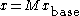. Consider the sequence of vectors 
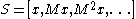obtained by repeatedly multiplying the vector by the matrix M; let y be any other vector of length n, and consider the sequence of finite-field elements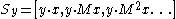 
We know that the matrix M has a minimal polynomial
; by the Cayley–Hamilton theorem
we know that this polynomial is of degree (which we will call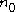
) no more than n. Say 
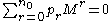. Then 
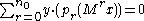; so the minimal polynomial of the matrix annihilates the sequence 
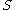and hence 
.
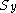But the Berlekamp–Massey algorithm allows us to calculate relatively efficiently some sequence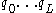
with 
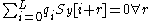. Our hope is that this sequence, which by construction annihilates 
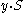, actually annihilates 
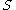; so we have 
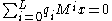. We then take advantage of the initial definition of 
to say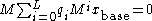 
and so 
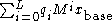is a hopefully non-zero kernel vector of 
.
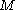It turns out, by a generalisation of the Berlekamp–Massey algorithm to provide a sequence of small matrices, that you can take the sequence produced for a large number of vectors and generate a kernel vector of the original large matrix. You need to compute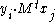
for some 
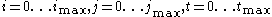where 
need to satisfy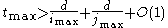 
and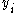 
are a series of vectors of length n; but in practice you can take 
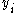as a sequence of unit vectors and simply write out the first 
entries in your vectors at each time t.
Don Coppersmith
Don Coppersmith is a cryptographer and mathematician. He was involved in the design of the Data Encryption Standard block cipher at IBM, particularly the design of the S-boxes, strengthening them against differential cryptanalysis...
.
Coppersmith's algorithm
Let M be an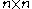 square matrix over some finite field F, let 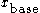be a random vector of length n, and let 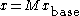. Consider the sequence of vectors 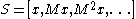obtained by repeatedly multiplying the vector by the matrix M; let y be any other vector of length n, and consider the sequence of finite-field elements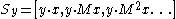 We know that the matrix M has a minimal polynomial
Minimal polynomial (linear algebra)
In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
; by the Cayley–Hamilton theorem
Cayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
we know that this polynomial is of degree (which we will call
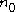) no more than n. Say 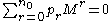. Then 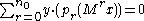; so the minimal polynomial of the matrix annihilates the sequence 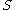and hence 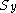.But the Berlekamp–Massey algorithm allows us to calculate relatively efficiently some sequence
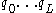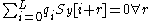with . Our hope is that this sequence, which by construction annihilates 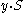, actually annihilates 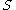; so we have 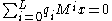. We then take advantage of the initial definition of to say 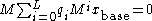and so 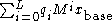is a hopefully non-zero kernel vector of 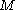.The block Wiedemann algorithm
The natural implementation of sparse matrix arithmetic on a computer makes it easy to compute the sequence S in parallel for a number of vectors equal to the width of a machine word – indeed, it will normally take no longer to compute for that many vectors than for one. If you have several processors, you can compute the sequence S for a different set of random vectors in parallel on all the computers.It turns out, by a generalisation of the Berlekamp–Massey algorithm to provide a sequence of small matrices, that you can take the sequence produced for a large number of vectors and generate a kernel vector of the original large matrix. You need to compute
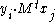for some 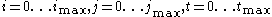where need to satisfy 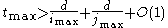and 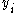are a series of vectors of length n; but in practice you can take 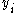as a sequence of unit vectors and simply write out the first entries in your vectors at each time t.