
Bertrand's postulate
Encyclopedia
Bertrand's postulate states that if n > 3 is an integer
, then there always exists at least one prime number
p with n < p < 2n − 2. A weaker but more elegant formulation is: for every n > 1 there is always at least one prime p such that n < p < 2n.
This statement was first conjectured in 1845 by Joseph Bertrand
(1822–1900). Bertrand himself verified his statement for all numbers in the interval [2, 3 × 106].
His conjecture was completely proved by Chebyshev
(1821–1894) in 1850 and so the postulate is also called the Bertrand-Chebyshev theorem or Chebyshev's theorem. Ramanujan (1887–1920) used properties of the Gamma function
to give a simpler proof, from which the concept of Ramanujan prime
s would later arise, and Erdős
(1913–1996) in 1932 published a simpler proof using the Chebyshev function
ϑ, defined as:
where p ≤ x runs over primes, and the binomial coefficient
s. See proof of Bertrand's postulate for the details.
s. Sylvester
(1814–1897) generalized it with the statement: the product of k consecutive integers greater than k is divisible by a prime greater than k.
).
The prime number theorem
(PNT) implies that the number of primes up to x is roughly x/log(x), so if we replace x with 2x then we see the number of primes up to 2x is asymptotically twice the number of primes up to x (the terms log(2x) and log(x) are asymptotically equivalent). Therefore the number of primes between n and 2n is roughly n/log(n) when n is large, and so in particular there are many more primes in this interval than are guaranteed by Bertrand's Postulate. So Bertrand's postulate is comparatively weaker than the PNT. But PNT is a deep theorem, while Bertrand's Postulate can be stated more memorably and proved more easily, and also makes precise claims about what happens for small values of n. (In addition, Chebyshev's theorem was proved before the PNT and so has historical interest.)
The similar and still unsolved Legendre's conjecture
asks whether for every n > 1, there is a prime p, such that n2 < p < (n + 1)2. Again we expect that there will be not just one but many primes between n2 and (n + 1)2, but in this case the PNT doesn't help: the number of primes up to x2 is asymptotic to x2/log(x2) while the number of primes up to (x + 1)2 is asymptotic to (x + 1)2/log((x + 1)2), which is asymptotic to the estimate on primes up to x2. So unlike the previous case of x and 2x we don't get a proof of Legendre's conjecture even for all large n. Error estimates on the PNT are not (indeed, cannot be) sufficient to prove the existence of even one prime in this interval.
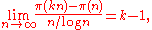
which implies that π(kn) − π(n) goes to infinity (and in particular is greater than 1 for sufficiently large n).
Non-asymptotic bounds have been also been proved. In 1952, Jitsuro Nagura proved that for n ≥ 25, there is always a prime between n and (1 + 1⁄5)n.
In 1976, Lowell Schoenfeld
showed that for n ≥ 2010760, there is always a prime between n and (1 + 1⁄16597)n. In 1998, Pierre Dusart
improved the result in his doctoral thesis, showing that for k ≥ 463, pk + 1 ≤ (1 + 1⁄(ln2 pk))pk, and in particular for x ≥ 3275, there exists a prime number between x and (1 + 1⁄(2ln2x))x. In 2010 he proved, that for x ≥ 396738 there is at least one prime between x and (1 + 1⁄(25ln2x))x.
Generalizations of Bertrand's Postulate have also been obtained by elementary methods. (In the following, n runs through the set of positive integers.) In 2006, M. El Bachraoui proved that there exists a prime between 2n and 3n.. In 2011, Andy Loo
proved that there exists a prime between 3n and 4n. Furthermore, he proved that as n tends to infinity, the number of primes between 3n and 4n also goes to infinity, thereby generalizing Erdős' and Ramanujan's results (see the section on Erdős' theorems above). None of these proofs require the use of deep analytic results.
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, then there always exists at least one prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p with n < p < 2n − 2. A weaker but more elegant formulation is: for every n > 1 there is always at least one prime p such that n < p < 2n.
This statement was first conjectured in 1845 by Joseph Bertrand
Joseph Louis François Bertrand
Joseph Louis François Bertrand was a French mathematician who worked in the fields of number theory, differential geometry, probability theory, economics and thermodynamics....
(1822–1900). Bertrand himself verified his statement for all numbers in the interval [2, 3 × 106].
His conjecture was completely proved by Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
(1821–1894) in 1850 and so the postulate is also called the Bertrand-Chebyshev theorem or Chebyshev's theorem. Ramanujan (1887–1920) used properties of the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
to give a simpler proof, from which the concept of Ramanujan prime
Ramanujan prime
In mathematics, a Ramanujan prime is a prime number that satisfies a result proven by Srinivasa Ramanujan relating to the prime-counting function.-Origins and definition:...
s would later arise, and Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
(1913–1996) in 1932 published a simpler proof using the Chebyshev function
Chebyshev function
[Image:ChebyshevPsi.png|thumb|right|The Chebyshev function ψ, with x [Image:ChebyshevPsi.png|thumb|right|The Chebyshev function ψ, with x ...
ϑ, defined as:
where p ≤ x runs over primes, and the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s. See proof of Bertrand's postulate for the details.
Sylvester's theorem
Bertrand's postulate was proposed for applications to permutation groupPermutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s. Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
(1814–1897) generalized it with the statement: the product of k consecutive integers greater than k is divisible by a prime greater than k.
Erdős's theorems
Erdős proved that for any positive integer k, there is a natural number N such that for all n > N, there are at least k primes between n and 2n. An equivalent statement had been proved earlier by Ramanujan (see Ramanujan primeRamanujan prime
In mathematics, a Ramanujan prime is a prime number that satisfies a result proven by Srinivasa Ramanujan relating to the prime-counting function.-Origins and definition:...
).
The prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
(PNT) implies that the number of primes up to x is roughly x/log(x), so if we replace x with 2x then we see the number of primes up to 2x is asymptotically twice the number of primes up to x (the terms log(2x) and log(x) are asymptotically equivalent). Therefore the number of primes between n and 2n is roughly n/log(n) when n is large, and so in particular there are many more primes in this interval than are guaranteed by Bertrand's Postulate. So Bertrand's postulate is comparatively weaker than the PNT. But PNT is a deep theorem, while Bertrand's Postulate can be stated more memorably and proved more easily, and also makes precise claims about what happens for small values of n. (In addition, Chebyshev's theorem was proved before the PNT and so has historical interest.)
The similar and still unsolved Legendre's conjecture
Legendre's conjecture
Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and 2 for every positive integer n. The conjecture is one of Landau's problems and unproven ....
asks whether for every n > 1, there is a prime p, such that n2 < p < (n + 1)2. Again we expect that there will be not just one but many primes between n2 and (n + 1)2, but in this case the PNT doesn't help: the number of primes up to x2 is asymptotic to x2/log(x2) while the number of primes up to (x + 1)2 is asymptotic to (x + 1)2/log((x + 1)2), which is asymptotic to the estimate on primes up to x2. So unlike the previous case of x and 2x we don't get a proof of Legendre's conjecture even for all large n. Error estimates on the PNT are not (indeed, cannot be) sufficient to prove the existence of even one prime in this interval.
Better results
It follows from the prime number theorem that for any real k > 1, there exists an n0 such that there is always a prime between n and kn for all n > n0: it can be shown, for instance, that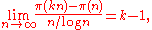
which implies that π(kn) − π(n) goes to infinity (and in particular is greater than 1 for sufficiently large n).
Non-asymptotic bounds have been also been proved. In 1952, Jitsuro Nagura proved that for n ≥ 25, there is always a prime between n and (1 + 1⁄5)n.
In 1976, Lowell Schoenfeld
Lowell Schoenfeld
Lowell Schoenfeld was an American mathematician known for his work in analytic number theory. He received his Ph.D. in 1944 from University of Pennsylvania under the direction of Hans Rademacher...
showed that for n ≥ 2010760, there is always a prime between n and (1 + 1⁄16597)n. In 1998, Pierre Dusart
Pierre Dusart
Pierre Dusart is a French mathematician at the Université de Limoges who specializes in number theory.-External links:* * Mathematics of Computation 68 , pp. 411–415.*...
improved the result in his doctoral thesis, showing that for k ≥ 463, pk + 1 ≤ (1 + 1⁄(ln2 pk))pk, and in particular for x ≥ 3275, there exists a prime number between x and (1 + 1⁄(2ln2x))x. In 2010 he proved, that for x ≥ 396738 there is at least one prime between x and (1 + 1⁄(25ln2x))x.
Generalizations of Bertrand's Postulate have also been obtained by elementary methods. (In the following, n runs through the set of positive integers.) In 2006, M. El Bachraoui proved that there exists a prime between 2n and 3n.. In 2011, Andy Loo
Andy Loo
Andy Loo is a Hong Kong mathematician working primarily in number theory. He is also a successful participant of the International Physics Olympiad.-Research:...
proved that there exists a prime between 3n and 4n. Furthermore, he proved that as n tends to infinity, the number of primes between 3n and 4n also goes to infinity, thereby generalizing Erdős' and Ramanujan's results (see the section on Erdős' theorems above). None of these proofs require the use of deep analytic results.
Consequences
- The sequence of primes, along with 1, is a complete sequenceComplete sequenceIn mathematics, an integer sequence is called a complete sequence if every positive integer can be expressed as a sum of values in the sequence, using each value at most once....
; any positive integer can be written as a sum of primes (and 1) using each at most once. - The number 1 is the only integer which is a harmonic number.


