
Bernstein's problem
Encyclopedia
In differential geometry, Bernstein's problem is as follows: if the graph of a function on Rn−1 is a minimal surface
in Rn, does this imply that the function is linear?
This is true in dimensions n at most 8, but false in dimensions n at least 9. The problem is named for Sergei Natanovich Bernstein
who solved the case n = 3.
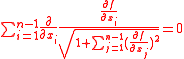
Bernstein's problem asks whether a function satisfying this equation is necessarily linear.
gave a new proof of Bernstein's theorem by deducing it from the fact that there is no minimal cone in R3.
showed that if there is no minimal cone in Rn−1 then the analogue of Bernstein's theorem is true in Rn, which in particular implies that it is true in R4.
showed there are no minimal cones in R4, thus extending Bernstein's theorem to R5.
showed there are no minimal cones in R7, thus extending Bernstein's theorem to R8. He also gave examples of locally stable cones in R8 and asked if they were global minima for area.
showed that Simon's cones are indeed globally of minimal area, and showed that in Rn for n≥9 there are graphs that are minimal but not hyperplanes. Combined with the result of Simons, this shows that the analogue of Bernstein's theorem is true in dimensions up to 8, and false in higher dimensions.
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
in Rn, does this imply that the function is linear?
This is true in dimensions n at most 8, but false in dimensions n at least 9. The problem is named for Sergei Natanovich Bernstein
Sergei Natanovich Bernstein
Sergei Natanovich Bernstein was a Russian and Soviet mathematician known for contributions to partial differential equations, differential geometry, probability theory, and approximation theory.-Partial differential equations:...
who solved the case n = 3.
Statement
Suppose that f is a function of n − 1 real variables. The graph of f is a surface in Rn, and the condition that this is a minimal surface is that f satisfies the minimal surface equation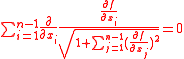
Bernstein's problem asks whether a function satisfying this equation is necessarily linear.
History
proved Bernstein's theorem that a graph of a real function on R2 that is also a minimal surface in R3 must be a plane.gave a new proof of Bernstein's theorem by deducing it from the fact that there is no minimal cone in R3.
showed that if there is no minimal cone in Rn−1 then the analogue of Bernstein's theorem is true in Rn, which in particular implies that it is true in R4.
showed there are no minimal cones in R4, thus extending Bernstein's theorem to R5.
showed there are no minimal cones in R7, thus extending Bernstein's theorem to R8. He also gave examples of locally stable cones in R8 and asked if they were global minima for area.
showed that Simon's cones are indeed globally of minimal area, and showed that in Rn for n≥9 there are graphs that are minimal but not hyperplanes. Combined with the result of Simons, this shows that the analogue of Bernstein's theorem is true in dimensions up to 8, and false in higher dimensions.

