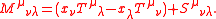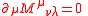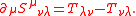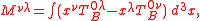Belinfante–Rosenfeld stress-energy tensor
Encyclopedia
In mathematical physics
, the Belinfante–Rosenfeld tensor is a modification of the energy-momentum tensor that is constructed from the canonical energy-momentum tensor and the spin current so as to be symmetric yet still conserved.
In a classical
or quantum
local field theory, the generator of Lorentz transformation
s can be written as an integral
of a local current
Here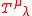
is the canonical Noether
energy-momentum tensor, and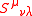
is the contribution of the intrinsic (spin) angular momentum
. Local conservation of angular momentum
requires that
Thus a source of spin-current implies a non-symmetric canonical energy-momentum tensor.
The Belinfante–Rosenfeld tensor is a modification of the energy momentum tensor
that is constructed from the canonical energy momentum tensor and the spin current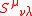
so as to be symmetric yet still conserved.
An integration by parts shows that
and so a physical interpretation of Belinfante tensor is that it includes the "bound momentum" associated with gradients of the intrinsic angular momentum. In other words, the added term is an analogue of the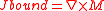
"bound current" associated with a magnetization density 
.
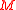The curious combination of spin-current components required to make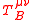
symmetric and yet still conserved seems totally ad hoc, but it was shown by both Rosenfeld and Belinfante that the modified tensor is precisely the symmetric Hilbert energy-momentum tensor that acts as the source of gravity in general relativity
. Just as it is the sum of the bound and free currents that acts as a source of the magnetic field, it is the sum of the bound and free energy-momentum that acts as a source of gravity.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the Belinfante–Rosenfeld tensor is a modification of the energy-momentum tensor that is constructed from the canonical energy-momentum tensor and the spin current so as to be symmetric yet still conserved.
In a classical
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
or quantum
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
local field theory, the generator of Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s can be written as an integral
of a local current
Here
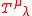is the canonical NoetherNoether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
energy-momentum tensor, and
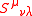is the contribution of the intrinsic (spin) angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. Local conservation of angular momentum
requires that
Thus a source of spin-current implies a non-symmetric canonical energy-momentum tensor.
The Belinfante–Rosenfeld tensor is a modification of the energy momentum tensor
that is constructed from the canonical energy momentum tensor and the spin current
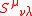so as to be symmetric yet still conserved.An integration by parts shows that
and so a physical interpretation of Belinfante tensor is that it includes the "bound momentum" associated with gradients of the intrinsic angular momentum. In other words, the added term is an analogue of the
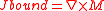"bound current" associated with a magnetization density 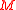.The curious combination of spin-current components required to make
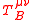symmetric and yet still conserved seems totally ad hoc, but it was shown by both Rosenfeld and Belinfante that the modified tensor is precisely the symmetric Hilbert energy-momentum tensor that acts as the source of gravity in general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Just as it is the sum of the bound and free currents that acts as a source of the magnetic field, it is the sum of the bound and free energy-momentum that acts as a source of gravity.