Bayes' rule
Encyclopedia
In probability theory
and applications, Bayes' rule relates the odds
of event
to event 
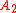, before and after conditioning
on event
. The relationship is expressed in terms of the Bayes factor,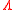 
. Bayes' rule is derived from and closely related to Bayes' theorem
. Bayes' rule may be preferred over Bayes' theorem when the relative probability (that is, the odds) of two events matters, but the individual probabilities do not. This is because in Bayes' rule,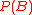
is eliminated and need not be calculated (see Derivation). It is commonly used in science
and engineering
, notably for model selection.
Under the frequentist interpretation of probability, Bayes' rule is a general relationship between
and 
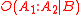, for any events 
, 
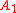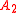and 
in the same event space. In this case,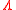 
represents the impact of the conditioning on the odds.
Under the Bayesian interpretation of probability
, Bayes' rule relates the odds on probability models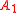
and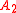 
before and after evidence 
is observed. In this case,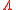 
represents the impact of the evidence on the odds. This is a form of Bayesian inference
- the quantity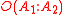
is called the prior odds, and 
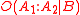the posterior odds. By analogy to the prior and posterior probability terms in Bayes' theorem
, Bayes' rule can be seen as Bayes' theorem in odds form. For more detail on the application of Bayes' rule under the Bayesian interpretation of probability, see Bayesian model selection.
, 
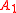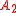and 
, Bayes' rule states that the conditional odds of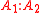 
given 
are equal to the marginal odds of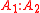 
multiplied by the Bayes factor
:
where
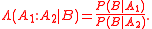
In the special case that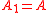
and 
, this may be written as
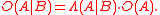
and 
,
where
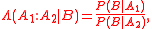
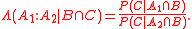
In this special case, the equivalent notation is
:
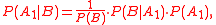
Combining these gives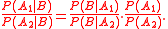
Now defining
this implies
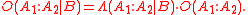
A similar derivation applies for conditioning on multiple events, using the appropriate extension of Bayes' theorem
Consider the drug testing example in the article on Bayes' theorem.
The same results may be obtained using Bayes' rule. The prior odds on an individual being a drug-user are 199 to 1 against, as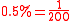
and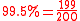 
. The Bayes factor
when an individual tests positive is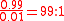
in favour of being a drug-user: this is the ratio of the probability of a drug-user testing positive, to the probability of a non-drug user testing positive. The posterior odds on being a drug user are therefore 
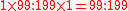, which is very close to 
. In round numbers, only one in three of those testing positive are actually drug-users.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and applications, Bayes' rule relates the odds
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
of event
to event 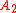, before and after conditioningConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
on event
. The relationship is expressed in terms of the Bayes factor, 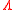. Bayes' rule is derived from and closely related to Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
. Bayes' rule may be preferred over Bayes' theorem when the relative probability (that is, the odds) of two events matters, but the individual probabilities do not. This is because in Bayes' rule,
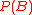is eliminated and need not be calculated (see Derivation). It is commonly used in scienceScience
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, notably for model selection.
Under the frequentist interpretation of probability, Bayes' rule is a general relationship between
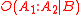and , for any events 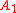, 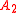and in the same event space. In this case, 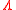represents the impact of the conditioning on the odds.Under the Bayesian interpretation of probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
, Bayes' rule relates the odds on probability models
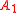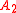and before and after evidence is observed. In this case, 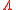represents the impact of the evidence on the odds. This is a form of Bayesian inferenceBayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
- the quantity
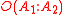is called the prior odds, and 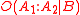the posterior odds. By analogy to the prior and posterior probability terms in Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
, Bayes' rule can be seen as Bayes' theorem in odds form. For more detail on the application of Bayes' rule under the Bayesian interpretation of probability, see Bayesian model selection.
Single event
Given events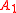, 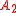and , Bayes' rule states that the conditional odds of 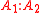given are equal to the marginal odds of 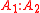multiplied by the Bayes factorBayes factor
In statistics, the use of Bayes factors is a Bayesian alternative to classical hypothesis testing. Bayesian model comparison is a method of model selection based on Bayes factors.-Definition:...
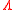:where
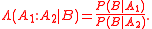
In the special case that
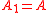and , this may be written as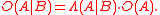Multiple events
Bayes' rule may be conditioned on an arbitrary number of events. For two events and ,where
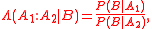
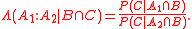
In this special case, the equivalent notation is
Derivation
Consider two instances of Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
:
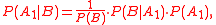
Combining these gives
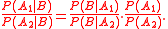
Now defining
this implies
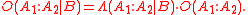
A similar derivation applies for conditioning on multiple events, using the appropriate extension of Bayes' theorem
Frequentist example
Consider the drug testing example in the article on Bayes' theorem.
The same results may be obtained using Bayes' rule. The prior odds on an individual being a drug-user are 199 to 1 against, as
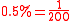and 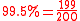. The Bayes factorBayes factor
In statistics, the use of Bayes factors is a Bayesian alternative to classical hypothesis testing. Bayesian model comparison is a method of model selection based on Bayes factors.-Definition:...
when an individual tests positive is
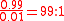in favour of being a drug-user: this is the ratio of the probability of a drug-user testing positive, to the probability of a non-drug user testing positive. The posterior odds on being a drug user are therefore 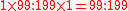, which is very close to . In round numbers, only one in three of those testing positive are actually drug-users.External links
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, discusses Bayesian model comparison in Chapters 3 and 28.