
Baire one star function
Encyclopedia
Baire one star function is a term from real analysis
. A function
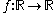 is in class Baire* one, written
is in class Baire* one, written 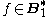 , and is called a Baire one star function, if for each perfect set
, and is called a Baire one star function, if for each perfect set 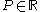 , there is an open interval
, there is an open interval 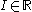 , such that
, such that 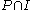 is nonempty, and the restriction
is nonempty, and the restriction  is continuous
is continuous
. The notion seems to have originated with B. Kerchheim in an article titled 'Baire one star functions' (Real Anal. Exch. 18 (1992/93), 385-399).
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
. A function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
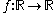 is in class Baire* one, written
is in class Baire* one, written 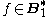 , and is called a Baire one star function, if for each perfect set
, and is called a Baire one star function, if for each perfect set 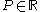 , there is an open interval
, there is an open interval 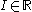 , such that
, such that 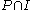 is nonempty, and the restriction
is nonempty, and the restriction  is continuous
is continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. The notion seems to have originated with B. Kerchheim in an article titled 'Baire one star functions' (Real Anal. Exch. 18 (1992/93), 385-399).

