
BCK algebra
Encyclopedia
In mathematics, BCI and BCK algebras are algebraic structures, introduced by Y. Imai, K. Iséki and S. Tanaka in 1966, that describe fragments of the propositional calculus involving implication known as BCI and BCK logics.
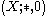 of type
of type 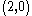 is called a BCI-algebra if, for any
is called a BCI-algebra if, for any 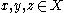 , it satisfies the following conditions:
, it satisfies the following conditions:
BCI-1: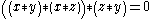
BCI-2:
BCI-3: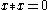
BCI-4: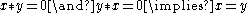
BCI-5:
 is called a BCK-algebra if it
is called a BCK-algebra if it
satisfies the following condition:
BCK-1: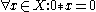
The subsets of a set form a BCK-algebra, where A*B is the difference
A\B (elements in A but not in B), and 0 is the empty set
.
A Boolean algebra is a BCK algebra if A*B is defined to be A∧¬B (A does not imply B).
BCI algebra
An algebra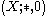 of type
of type 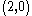 is called a BCI-algebra if, for any
is called a BCI-algebra if, for any 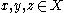 , it satisfies the following conditions:
, it satisfies the following conditions:BCI-1:
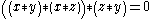
BCI-2:

BCI-3:
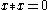
BCI-4:
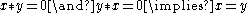
BCI-5:

BCK algebra
A BCI-algebra is called a BCK-algebra if it
is called a BCK-algebra if itsatisfies the following condition:
BCK-1:
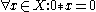
Examples
Every abelian group of is a BCI-algebra, with * group subtraction and 0 the group identity.The subsets of a set form a BCK-algebra, where A*B is the difference
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
A\B (elements in A but not in B), and 0 is the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
.
A Boolean algebra is a BCK algebra if A*B is defined to be A∧¬B (A does not imply B).

