
A¹ homotopy theory
Encyclopedia
In algebraic geometry
and algebraic topology
, a branch of mathematics
, A1 homotopy theory is a way to apply the techniques of algebraic topology, specifically homotopy
, to algebraic varieties and, more generally, to schemes
. The theory is due to Fabien Morel and Vladimir Voevodsky
. The underlying idea is that it should be possible to develop a purely algebraic approach to homotopy theory by replacing the unit interval [0,1], which is not an algebraic variety, with the affine line A1, which is. The theory requires a substantial amount of technique to set up, but has spectacular applications such as Voevodsky's construction of the derived category
of mixed motives.
Most of the construction works for any site
T. Assume that the site is subcanonical
, and let Shv(T) be the category of sheaves of sets on this site. This category is too restrictive, so we will need to enlarge it. Let Δ be the simplicial category
, that is, the category whose objects are the sets {0}, {0, 1}, {0, 1, 2}, and so on, and whose morphisms are order-preserving functions. We let ΔopShv(T) denote the category of functors Δop → Shv(T). That is, ΔopShv(T) is the category of simplicial objects on Shv(T). Such an object is also called a simplicial sheaf on T. The category of all simplicial sheaves on T is a Grothendieck topos.
A point of a site T is a geometric morphism x* : Shv(T) → Set, where Set is the category of sets. We will define a closed model structure on ΔopShv(T) in terms of points. Let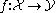 be a morphism of simplicial sheaves. We say that:
be a morphism of simplicial sheaves. We say that:
The homotopy category of this model structure is denoted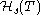 .
.
This model structure will not give the right homotopy category because it does not pay any attention to the unit interval object. Call this object I, and denote the final object of T by pt. We assume that I comes with a map μ : I × I → I and two maps i0, i1 : pt → I such that:
Now we localize the homotopy theory with respect to I. A simplicial sheaf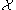 is called I-local if for any simplicial sheaf
is called I-local if for any simplicial sheaf 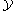 the map
the map
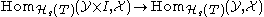
induced by i0 : pt → I is a bijection. A morphism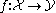 is an I-weak equivalence if for any I-local
is an I-weak equivalence if for any I-local 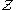 , the induced map
, the induced map
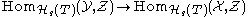
is a bijection. The homotopy theory of the site with interval (T, I) is the localization of ΔopShv(T) with respect to I-weak equivalences. This category is called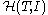 .
.
Finally we may define the A1 homotopy category. Let S be a finite dimensional Noetherian scheme, and let Sm/S denote the category of smooth schemes over S. Equip Sm/S with the Nisnevich topology
to get the site (Sm/S)Nis. We let the affine line A1 play the role of the interval. The above construction determines a closed model structure on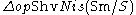 , and the corresponding homotopy category is called the A1 homotopy category.
, and the corresponding homotopy category is called the A1 homotopy category.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, A1 homotopy theory is a way to apply the techniques of algebraic topology, specifically homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
, to algebraic varieties and, more generally, to schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. The theory is due to Fabien Morel and Vladimir Voevodsky
Vladimir Voevodsky
Vladimir Voevodsky is a Russian American mathematician. His work in developing a homotopy theory for algebraic varieties and formulating motivic cohomology led to the award of a Fields Medal in 2002.- Biography :...
. The underlying idea is that it should be possible to develop a purely algebraic approach to homotopy theory by replacing the unit interval [0,1], which is not an algebraic variety, with the affine line A1, which is. The theory requires a substantial amount of technique to set up, but has spectacular applications such as Voevodsky's construction of the derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of mixed motives.
Construction of the A1 homotopy category
A1 homotopy theory is founded on a category called the A1 homotopy category. This is the homotopy category for a certain closed model category whose construction requires several steps.Most of the construction works for any site
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...
T. Assume that the site is subcanonical
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...
, and let Shv(T) be the category of sheaves of sets on this site. This category is too restrictive, so we will need to enlarge it. Let Δ be the simplicial category
Simplicial category
In mathematics, the simplex category is the category of finite ordinals and order preserving maps. It is used to define simplicial and cosimplicial objects.-Formal definition:...
, that is, the category whose objects are the sets {0}, {0, 1}, {0, 1, 2}, and so on, and whose morphisms are order-preserving functions. We let ΔopShv(T) denote the category of functors Δop → Shv(T). That is, ΔopShv(T) is the category of simplicial objects on Shv(T). Such an object is also called a simplicial sheaf on T. The category of all simplicial sheaves on T is a Grothendieck topos.
A point of a site T is a geometric morphism x* : Shv(T) → Set, where Set is the category of sets. We will define a closed model structure on ΔopShv(T) in terms of points. Let
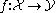 be a morphism of simplicial sheaves. We say that:
be a morphism of simplicial sheaves. We say that:
- f is a weak equivalence if, for any point x of T, the morphism of simplicial setSimplicial setIn mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
s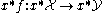 is a weak equivalence.
is a weak equivalence. - f is a cofibration if it is a monomorphism.
- f is a fibration if it has the right lifting property with respect to any cofibration which is a weak equivalence.
The homotopy category of this model structure is denoted
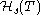 .
.This model structure will not give the right homotopy category because it does not pay any attention to the unit interval object. Call this object I, and denote the final object of T by pt. We assume that I comes with a map μ : I × I → I and two maps i0, i1 : pt → I such that:
- If p is the canonical morphism I → pt, then
- μ(i0 × 1I) = μ(1I × i0) = i0p.
- μ(i1 × 1I) = μ(1I × i1) = 1I.
- The morphism
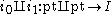 is a monomorphism.
is a monomorphism.
Now we localize the homotopy theory with respect to I. A simplicial sheaf
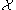 is called I-local if for any simplicial sheaf
is called I-local if for any simplicial sheaf 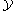 the map
the map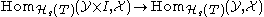
induced by i0 : pt → I is a bijection. A morphism
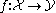 is an I-weak equivalence if for any I-local
is an I-weak equivalence if for any I-local 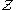 , the induced map
, the induced map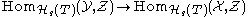
is a bijection. The homotopy theory of the site with interval (T, I) is the localization of ΔopShv(T) with respect to I-weak equivalences. This category is called
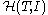 .
.Finally we may define the A1 homotopy category. Let S be a finite dimensional Noetherian scheme, and let Sm/S denote the category of smooth schemes over S. Equip Sm/S with the Nisnevich topology
Nisnevich topology
In algebraic geometry, the Nisnevich topology, sometimes called the completely decomposed topology, is a Grothendieck topology on the category of schemes which has been used in algebraic K-theory, A¹ homotopy theory, and the theory of motives...
to get the site (Sm/S)Nis. We let the affine line A1 play the role of the interval. The above construction determines a closed model structure on
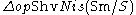 , and the corresponding homotopy category is called the A1 homotopy category.
, and the corresponding homotopy category is called the A1 homotopy category.

