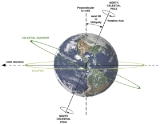
Axial tilt
Overview
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, axial tilt (also called obliquity) is the angle between an object's rotational axis, and a line perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to its orbital plane
Orbital plane (astronomy)
All of the planets, comets, and asteroids in the solar system are in orbit around the Sun. All of those orbits line up with each other making a semi-flat disk called the orbital plane. The orbital plane of an object orbiting another is the geometrical plane in which the orbit is embedded...
. It differs from inclination
Inclination
Inclination in general is the angle between a reference plane and another plane or axis of direction.-Orbits:The inclination is one of the six orbital parameters describing the shape and orientation of a celestial orbit...
.
To measure obliquity, use the right hand grip rule for both the rotation and the orbital motion, i.e.: the line from the vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
at the object's centre to its north pole
Poles of astronomical bodies
The poles of astronomical bodies are determined based on their axis of rotation in relation to the celestial poles of the celestial sphere.-Geographic poles:...
(above which the object appears to rotate counter-clockwise); and the line drawn from the vertex in the direction of the normal to its orbital plane, (above which the object moves counter-clockwise in its orbit).

