
Avrami equation
Encyclopedia

The equation is also known as the Johnson-Mehl-Avrami-Kolmogorov, or JMAK, equation. The equation was popularized by Melvin Avrami in a series of papers published in the Journal of Chemical Physics
Journal of Chemical Physics
The Journal of Chemical Physics is a scientific journal that publishes research papers on all areas of chemical physics. Two volumes, each of 24 issues, are published per year. It is published by the American Institute of Physics. The editors have been:...
from 1939 to 1941.
Transformation Kinetics

The initial slow rate can be attributed to the time required for a significant number of nuclei of the new phase to form and begin growing. During the intermediate period the transformation is rapid as the nuclei grow into particles and consume the old phase while nuclei continue to form in the remaining parent phase.
Once the transformation begins to near completion there is little untransformed material for nuclei to form in and the production of new particles begins to slow. Further, the particles already existing begin to touch one another, forming a boundary where growth stops.
Derivation
The simplest derivation of the Avrami equation makes a number of significant assumptions and simplifications :- Nucleation occurs randomly and homogeneously over the entire untransformed portion of the material
- The growth rate does not depend on the extent of transformation
- Growth occurs at the same rate in all directions
If these conditions are met then a transformation of
 into
into 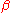 will proceed by the nucleation of new particles at a rate
will proceed by the nucleation of new particles at a rate 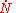 per unit volume which grow at a rate
per unit volume which grow at a rate  into spherical particles and only stop growing when they impinge upon each other. During a time interval,
into spherical particles and only stop growing when they impinge upon each other. During a time interval,  , nucleation and growth can only take place in untransformed material. However, the problem is more easily solved by applying the concept of an extended volume - the volume of the new phase that would form if the entire sample was still untransformed. During the time interval τ to τ+dτ the number of nuclei, N, that appear in a sample of volume V will be given by:
, nucleation and growth can only take place in untransformed material. However, the problem is more easily solved by applying the concept of an extended volume - the volume of the new phase that would form if the entire sample was still untransformed. During the time interval τ to τ+dτ the number of nuclei, N, that appear in a sample of volume V will be given by: [1]
[1]Since growth is isotropic, constant and unhindered by previously transformed material each nuclei will grow into a sphere of radius
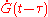 and so the extended volume of
and so the extended volume of 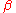 due to nuclei appearing in the time interval will be:
due to nuclei appearing in the time interval will be: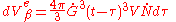
The integration of this equation between
 and
and  will yield the total extended volume that appears in the time interval
will yield the total extended volume that appears in the time interval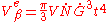
Only a fraction of this extended volume is real; some portion of it lies on previously transformed material and is virtual. Since nucleation occurs randomly, the fraction of the extended volume that forms during each time increment that is real will be proportional to the volume fraction of untransformed
 . Thus
. Thus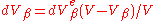
and upon integration
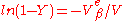
where Y is the volume fraction of
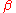 (
(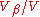 ).
).Given the previous equations this can be reduced to the more familiar form of the Avrami (JMAK) equation which gives the fraction of transformed material after a hold time at a given temperature
 where
where  and
and 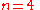
This can be rewritten as:
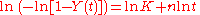
which allows the determination of the constants n and k from a plot of lnln(1/(1-Y)) vs ln(t). If the transformation follows the Avrami equation this yields a straight line with gradient n and intercept ln K.
Interpretation of Avrami constants
The physical interpretation of the Avrami constants, k and n, is difficult and open to interpretation. Originally, n was held to have an integer value between 1-4 which reflected the nature of the transformation in question. In the derivation above, for example, the value of 4 can be said to have contributions from three dimensions of growth and one representing a constant nucleation rate. Alternative derivations exist where n has a different value.If the nuclei are preformed, and so all present from the beginning, the transformation is only due to the 3-dimensional growth of the nuclei and n has a value of 3.
An interesting condition occurs when nucleation occurs on specific sites (such as grain boundaries
Grain boundary
A grain boundary is the interface between two grains, or crystallites, in a polycrystalline material. Grain boundaries are defects in the crystal structure, and tend to decrease the electrical and thermal conductivity of the material...
or impurities) which rapidly saturate soon after the transformation begins. Initially, nucleation may be random and growth unhindered leading to high values for n (3,4). Once the nucleation sites are consumed the formation of new particles will cease.
Furthermore, if the distribution of nucleation sites is non-random then the growth may be restricted to 1 or 2-dimensions. Site saturation may lead to n values of 1, 2 or 3 for surface, edge and point sites, respectively.

