Asymptotology
Encyclopedia
Asymptotology has been defined as “the art of dealing with applied mathematical systems in limiting cases” as well as “the science about the synthesis of simplicity and exactness by means of localization.
with the introduction of the asymptote
, a line to which a curve tends at infinity. The word Ασύμπτωτος (asymptotos) in Greek means non-coincident and puts strong emphasis on the point that approximation does not turn into coincidence. It is a salient feature of asymptotics, but this property alone does not entirely cover the idea of asymptotics and, etymologically, the term seems to be quite insufficient.
and other fields of science
, one frequently comes across problems of an asymptotic nature, such as damping, orbiting, stabilization of a perturbed motion, etc. Their solutions lend themselves to asymptotic analysis
(perturbation theory
), which is widely used in modern applied mathematics
, mechanics
and physics
. But asymptotic methods put a claim on being more than a part of classical mathematics. K. Friedrichs said: “Asymptotic description is not only a convenient tool in the mathematical analysis of nature, it has some more fundamental significance”. M. Kruskal
introduced the special term asymptotology, defined above, and called for a formalization of the accumulated experience to convert the art of asymptotology to a science.
A general term is capable of possessing significant heuristic value. In his essay The Future of Mathematics, H. Poincaré wrote:
The invention of a new word will often be sufficient to bring out the relation, and the word will be creative... It is hardly possible to believe what economy of thought, as Mach used to say, can be effected by a well-chosen term... Mathematics is the art of giving the same name to different things... When language has been well chosen, one is astonished to find that all demonstrations made for a known object apply immediately to many new objects: nothing requires to be changed, not even the terms, since the names have become the same... The bare fact, then, has sometimes no great interest: ... it only acquires a value when some more careful thinker perceives the connection it brings out, and symbolizes it by a term.
Problems of asymptotic nature, such as damping, orbiting, stabilization of a perturbed motion, are encountered in physics and other fields. Asymptotic analysis
(perturbation theory) is widely used in the modern applied mathematics
, mechanics and physics. But asymptotic methods put a claim on being more than a part of classical mathematics
; K.Friedrichs said: “Asymptotic description is not only a convenient tool in the mathematical analysis
of nature, it has some more fundamental significance”. M.Kruskal introduced a special term “asymptotology” and defined it as an art of handling applied mathematical systems in limiting cases. He called for a formalization of the accumulated experience to convert the art of asymptotology to science.
In addition, “the success of ‘cybernetics
’, ‘attractors’ and ‘catastrophe theory
’ illustrates the fruitfulness of word creation as scientific research” .
Almost every physical theory, formulated in the most general manner, is rather difficult from a mathematical point of view. Therefore both at the genesis of the theory and its further development, the simplest limiting cases, which allow analytical solutions, are of particular importance. In those limits, the number of equations usually decreases, their order reduces, nonlinear equations can be replaced by linear ones, the initial system becomes averaged in a certain sense, and so on.
All these idealizations, different as they may seem, increase the degree of symmetry of the mathematical model of the phenomenon under consideration.
In attempting to obtain a better approximation of the exact solution to the given problem, it is crucial that the determination of corrective solutions, which depart from the limit case, be much simpler than directly investigating the governing system. At first sight, the possibilities of such an approach seem restricted to varying the parameters determining the system only within a narrow range. However, experience in the investigation of different physical problems shows that if the system’s parameters have changed sufficiently and the system has deviated far from the symmetrical limit case, another limit system, often with less obvious symmetries can be found, to which an asymptotic analysis is also applicable. This allows one to describe the system’s behavior on the basis of a small number of limit cases over the whole range of parameter variations. Such an approach corresponds to the maximum level of intuition, promotes further insights, and eventually leads to the formulation of new physical concepts. It is also important that asymptotic methods help to establish the connection between different physical theories.
The aim of the asymptotic approach is to simplify the object. This simplification is attained by decreasing the vicinity of the singularity under consideration. It is typical that the accuracy of asymptotic expansions grows with localization. Exactness and simplicity are commonly regarded as mutually exclusive notions. When tending to simplicity, we sacrifice exactness, and trying to achieve exactness, we expect no simplicity. Under localization
, however, the antipodes converge; the contradiction is resolved in a synthesis called asymptotics. In other words, simplicity and exactness are coupled by an “uncertainty principle” relation while the domain size serves as a small parameter - a measure of uncertainty.
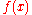in an asymptotic sequence 
:
, 
→ 
.
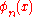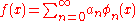A partial sum of the series is designated by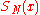
, and the exactness of approximation at a given 
is estimated by 
. Simplicity is characterized here by the number 
and the locality by the length of interval 
.
Based on known properties of the asymptotic expansion
, we consider the pair wise interrelation of values
, 
, and 
. At a fixed 
the expansion initially converges, i.e., the exactness increases at the cost of simplicity. If we fix 
, the exactness and the interval size begin to compete. The smaller the interval, the given value of 
is reached more simply.
We illustrate these regularities using a simple example. Consider the integral exponential function:
, 
.
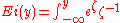Integrating by parts, we obtain the following asymptotic expansion
, 
→ 
.
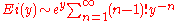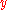Put
, 
. Calculating the partial sums of this series and the values 
and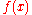 
for different 
yields:
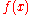
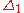
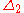
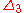
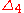
1/3 0,262 0,071 0,040 0,034 0,040 0,060 0,106 0,223
1/5 0,171 0,029 0,011 0,006 0,004 0,0035 0,0040 0,0043
1/7 0,127 0,016 0,005 0,002 0,001 0,0006 0,0005 0,0004
Thus, at a given
, the exactness first increases with the growth of 
and then decreases (so one has an asymptotic expansion). For a given 
, one may observe an improvement of exactness with diminishing 
.
Finally, is it worth using asymptotic methods if computers and numerical procedures have reached such an advanced state? As D.G. Crighton
has mentioned,
Design of computational or experimental schemes without the guidance of asymptotic information is wasteful at best, dangerous at worst, because of the possible failure to identify crucial (stiff) features of the process and their localization in coordinate and parameter space. Moreover, all experience suggests that asymptotic solutions are useful numerically far beyond their nominal range of validity, and can often be used directly, at least at a preliminary product design stage, for example, saving the need for accurate computation until the final design stage where many variables have been restricted to narrow ranges.
So, had he lived now, Galileo would have said: "The book of Nature
is written in the language of asymptotology".
Principles
The field of asymptotics is normally first encountered in school geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
with the introduction of the asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
, a line to which a curve tends at infinity. The word Ασύμπτωτος (asymptotos) in Greek means non-coincident and puts strong emphasis on the point that approximation does not turn into coincidence. It is a salient feature of asymptotics, but this property alone does not entirely cover the idea of asymptotics and, etymologically, the term seems to be quite insufficient.
Perturbation theory, small and large parameters
In physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and other fields of science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
, one frequently comes across problems of an asymptotic nature, such as damping, orbiting, stabilization of a perturbed motion, etc. Their solutions lend themselves to asymptotic analysis
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
(perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
), which is widely used in modern applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. But asymptotic methods put a claim on being more than a part of classical mathematics. K. Friedrichs said: “Asymptotic description is not only a convenient tool in the mathematical analysis of nature, it has some more fundamental significance”. M. Kruskal
Martin Kruskal
Martin David Kruskal was an American mathematician and physicist. He made fundamental contributions in many areas of mathematics and science, ranging from plasma physics to general relativity and from nonlinear analysis to asymptotic analysis...
introduced the special term asymptotology, defined above, and called for a formalization of the accumulated experience to convert the art of asymptotology to a science.
A general term is capable of possessing significant heuristic value. In his essay The Future of Mathematics, H. Poincaré wrote:
The invention of a new word will often be sufficient to bring out the relation, and the word will be creative... It is hardly possible to believe what economy of thought, as Mach used to say, can be effected by a well-chosen term... Mathematics is the art of giving the same name to different things... When language has been well chosen, one is astonished to find that all demonstrations made for a known object apply immediately to many new objects: nothing requires to be changed, not even the terms, since the names have become the same... The bare fact, then, has sometimes no great interest: ... it only acquires a value when some more careful thinker perceives the connection it brings out, and symbolizes it by a term.
Problems of asymptotic nature, such as damping, orbiting, stabilization of a perturbed motion, are encountered in physics and other fields. Asymptotic analysis
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
(perturbation theory) is widely used in the modern applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, mechanics and physics. But asymptotic methods put a claim on being more than a part of classical mathematics
Classical mathematics
In the foundations of mathematics, classical mathematics refers generally to the mainstream approach to mathematics, which is based on classical logic and ZFC set theory. It stands in contrast to other types of mathematics such as constructive mathematics or predicative mathematics; theories other...
; K.Friedrichs said: “Asymptotic description is not only a convenient tool in the mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
of nature, it has some more fundamental significance”. M.Kruskal introduced a special term “asymptotology” and defined it as an art of handling applied mathematical systems in limiting cases. He called for a formalization of the accumulated experience to convert the art of asymptotology to science.
In addition, “the success of ‘cybernetics
Cybernetics
Cybernetics is the interdisciplinary study of the structure of regulatory systems. Cybernetics is closely related to information theory, control theory and systems theory, at least in its first-order form...
’, ‘attractors’ and ‘catastrophe theory
Catastrophe theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry....
’ illustrates the fruitfulness of word creation as scientific research” .
Almost every physical theory, formulated in the most general manner, is rather difficult from a mathematical point of view. Therefore both at the genesis of the theory and its further development, the simplest limiting cases, which allow analytical solutions, are of particular importance. In those limits, the number of equations usually decreases, their order reduces, nonlinear equations can be replaced by linear ones, the initial system becomes averaged in a certain sense, and so on.
All these idealizations, different as they may seem, increase the degree of symmetry of the mathematical model of the phenomenon under consideration.
Asymptotic approach
In essence, the asymptotic approach to a complex problem consists in treating the insufficiently symmetrical governing system as close to a certain symmetrical one as possible.In attempting to obtain a better approximation of the exact solution to the given problem, it is crucial that the determination of corrective solutions, which depart from the limit case, be much simpler than directly investigating the governing system. At first sight, the possibilities of such an approach seem restricted to varying the parameters determining the system only within a narrow range. However, experience in the investigation of different physical problems shows that if the system’s parameters have changed sufficiently and the system has deviated far from the symmetrical limit case, another limit system, often with less obvious symmetries can be found, to which an asymptotic analysis is also applicable. This allows one to describe the system’s behavior on the basis of a small number of limit cases over the whole range of parameter variations. Such an approach corresponds to the maximum level of intuition, promotes further insights, and eventually leads to the formulation of new physical concepts. It is also important that asymptotic methods help to establish the connection between different physical theories.
The aim of the asymptotic approach is to simplify the object. This simplification is attained by decreasing the vicinity of the singularity under consideration. It is typical that the accuracy of asymptotic expansions grows with localization. Exactness and simplicity are commonly regarded as mutually exclusive notions. When tending to simplicity, we sacrifice exactness, and trying to achieve exactness, we expect no simplicity. Under localization
Localization
Localization or localisation, and represented as a numeronym as L10n, may refer to:* Language localization, the process of translating a product into different languages or adapting a product for a specific country or region...
, however, the antipodes converge; the contradiction is resolved in a synthesis called asymptotics. In other words, simplicity and exactness are coupled by an “uncertainty principle” relation while the domain size serves as a small parameter - a measure of uncertainty.
Asymptotic uncertainty principle
Let us illustrate the “asymptotic uncertainty principle”. Take the expansion of the function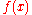 in an asymptotic sequence 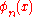: 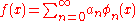, → .A partial sum of the series is designated by
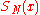, and the exactness of approximation at a given is estimated by . Simplicity is characterized here by the number and the locality by the length of interval .Based on known properties of the asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
, we consider the pair wise interrelation of values
, , and . At a fixed the expansion initially converges, i.e., the exactness increases at the cost of simplicity. If we fix , the exactness and the interval size begin to compete. The smaller the interval, the given value of is reached more simply.We illustrate these regularities using a simple example. Consider the integral exponential function:
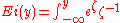, .Integrating by parts, we obtain the following asymptotic expansion
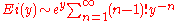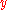, → .Put
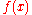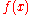
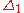
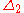
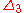
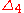
, . Calculating the partial sums of this series and the values and for different yields: 1/3 0,262 0,071 0,040 0,034 0,040 0,060 0,106 0,223
1/5 0,171 0,029 0,011 0,006 0,004 0,0035 0,0040 0,0043
1/7 0,127 0,016 0,005 0,002 0,001 0,0006 0,0005 0,0004
Thus, at a given
, the exactness first increases with the growth of and then decreases (so one has an asymptotic expansion). For a given , one may observe an improvement of exactness with diminishing .Finally, is it worth using asymptotic methods if computers and numerical procedures have reached such an advanced state? As D.G. Crighton
David Crighton
David George Crighton FRS was a British mathematician and physicist.- Life :...
has mentioned,
Design of computational or experimental schemes without the guidance of asymptotic information is wasteful at best, dangerous at worst, because of the possible failure to identify crucial (stiff) features of the process and their localization in coordinate and parameter space. Moreover, all experience suggests that asymptotic solutions are useful numerically far beyond their nominal range of validity, and can often be used directly, at least at a preliminary product design stage, for example, saving the need for accurate computation until the final design stage where many variables have been restricted to narrow ranges.
So, had he lived now, Galileo would have said: "The book of Nature
Nature
Nature, in the broadest sense, is equivalent to the natural world, physical world, or material world. "Nature" refers to the phenomena of the physical world, and also to life in general...
is written in the language of asymptotology".