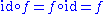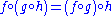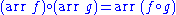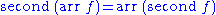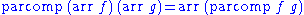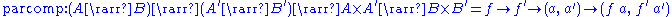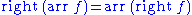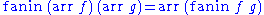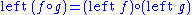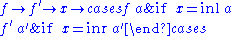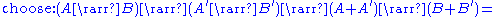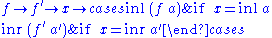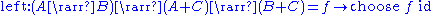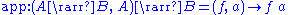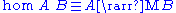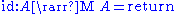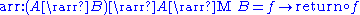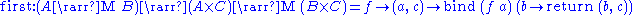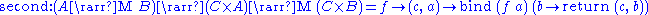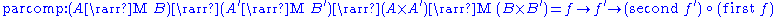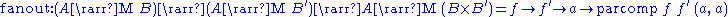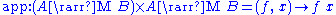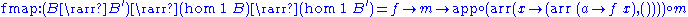Arrows in functional programming
Encyclopedia
In computer science
, arrows provide a more general interface to computation than monads
. Monads essentially provide a sequential interface to computation
: one can build a computation out of a value, or sequence two computations. Arrows provide more possibilities, including expressing (true, nondeterministic) parallel computation. Indeed, monads turn out to be equivalent to arrows of a particular kind, ArrowApply. Because arrows carry more type information than just the result type, composition can be more efficient—for example, eliminating space leaks.
Arrows have found use in functional reactive programming
.
subject to the following laws:
Note that
defines a category of types, with the obvious choices for 
and 
.
Alternative notations are defined for the composition operator:
.
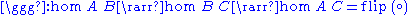An arrow is a category of types endowed with the following functions:
subject to the following laws:
where the
category of types is extended to an arrow as follows:
subject to the following laws:
where the
arrow is endowed with the following definition:
The
arrow has an application morphism, apply:
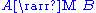form a category of types, called the Kleisli category
for the monad. Its definition is as follows:
The Kleisli category is also an arrow:
The Kleisli category is an arrow with choice:
The Kleisli category is an arrow with application:
Conversely, given any arrow with application, the corresponding monad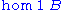
(where 
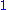denotes the unit type
) is defined by the following functions:
The fmap and join functions are:
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, arrows provide a more general interface to computation than monads
Monads in functional programming
In functional programming, a monad is a programming structure that represents computations. Monads are a kind of abstract data type constructor that encapsulate program logic instead of data in the domain model...
. Monads essentially provide a sequential interface to computation
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
: one can build a computation out of a value, or sequence two computations. Arrows provide more possibilities, including expressing (true, nondeterministic) parallel computation. Indeed, monads turn out to be equivalent to arrows of a particular kind, ArrowApply. Because arrows carry more type information than just the result type, composition can be more efficient—for example, eliminating space leaks.
Arrows have found use in functional reactive programming
Functional reactive programming
Functional reactive programming is a programming paradigm for reactive programming using the building blocks of functional programmingThe key points of FRP are:* Input is viewed as a "behavior", or time-varying stream of events...
.
Definition
As a prerequisite, we define a category of types. It is given by:- a type constructorType constructorIn the area of mathematical logic and computer science known as type theory, a type constructor is a feature of a typed formal language that builds new types from old. Typical type constructors encountered are product types, function types, power types and list types. Basic types are considered...
which takes two type parameters - for any type A, an object
- for any three types A, B, C an operator
subject to the following laws:
Note that
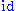defines a category of types, with the obvious choices for and .Alternative notations are defined for the composition operator:
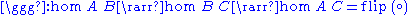.An arrow is a category of types endowed with the following functions:
;
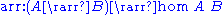
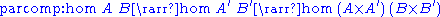
subject to the following laws:
where the
category of types is extended to an arrow as follows:
Arrows with choice
We may extend the arrow construct with the ability to choose between alternative computation paths. An arrow with choice is characterized by the following functions:
;
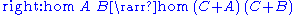
subject to the following laws:
where the
arrow is endowed with the following definition:
Arrows with application
Arrows with application extend the basic arrow type with an application morphism:
The
arrow has an application morphism, apply:
Kleisli arrows
For any monad M, functions of type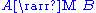 form a category of types, called the Kleisli categoryKleisli category
In category theory, a Kleisli category is a category naturally associated to any monad T. It is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the...
for the monad. Its definition is as follows:
The Kleisli category is also an arrow:
The Kleisli category is an arrow with choice:
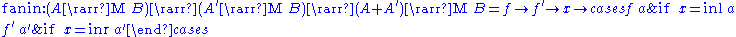
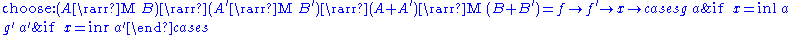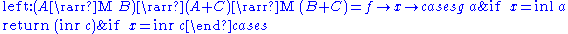where 
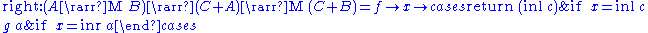where 
where 
The Kleisli category is an arrow with application:
Conversely, given any arrow with application, the corresponding monad
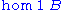(where 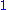denotes the unit typeUnit type
In the area of mathematical logic, and computer science known as type theory, a unit type is a type that allows only one value . The carrier associated with a unit type can be any singleton set. There is an isomorphism between any two such sets, so it is customary to talk about the unit type and...
) is defined by the following functions:
The fmap and join functions are:
External links
- Arrows: A General Interface to Computation
- “Generalising Monads to Arrows”, John HughesJohn Hughes (computer scientist)R. John M. Hughes is a computer scientist who does research in the field of programming languages and the author of several influential research papers on the subject, including "Why Functional Programming Matters". He is a professor in the department of Computing Science at the Chalmers University...
, in Science of Computer Programming 37, pp67–111, May 2000. - A New Notation for Arrows, Ross Paterson, in ICFP, Sep 2001.
- Arrows and Computation, Ross Paterson, in The Fun of Programming, Palgrave, 2003.
- Arrow notation ghc manual