Argument of periapsis
Encyclopedia
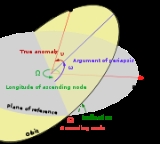
The argument of periapsis (also called argument of perifocus or argument of pericenter), symbolized as ω, is one of the orbital elements of an orbit
ing body. Specifically, ω is the angle between the orbit's periapsis
(the point of closest approach to the central point) and the orbit's ascending node (the point where the body crosses the plane of reference
from South to North). The angle is measured in the orbital plane
and in the direction of motion. For specific types of orbits, words such as "perihelion" (for Sun
-centered orbits), "perigee" (for Earth
-centered orbits), "periastron" (for orbits around stars) and so on may replace the word "periapsis". See apsis
for more information.
An argument of periapsis of 0° means that the orbiting body will be at its closest approach to the central body at the same moment that it crosses the plane of reference from South to North. An argument of periapsis of 90° means that the orbiting body will reach periapsis at its northmost distance from the plane of reference.
Adding the argument of periapsis to the longitude of the ascending node
gives the longitude of the periapsis
. However, especially in discussions of binary stars and exoplanets, the terms "longitude of periapsis" or "longitude of periastron" are often used synonymously with "argument of periapsis".
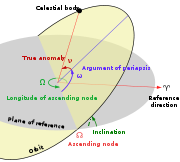
the argument of periapsis ω can be calculated as follows:
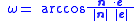
where:
In the case of equatorial orbits, though the argument is strictly undefined, it is often assumed that:
where:
In the case of circular orbits it is often assumed that the periapsis is placed at the ascending node and therefore ω=0.
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
ing body. Specifically, ω is the angle between the orbit's periapsis
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
(the point of closest approach to the central point) and the orbit's ascending node (the point where the body crosses the plane of reference
Plane of reference
A term used in celestial mechanics, the plane of reference is the plane by means of which orbital elements are defined. The two main orbital elements that are measured with respect to the plane of reference are the inclination and the longitude of the ascending node.Depending on the type of body...
from South to North). The angle is measured in the orbital plane
Orbital plane (astronomy)
All of the planets, comets, and asteroids in the solar system are in orbit around the Sun. All of those orbits line up with each other making a semi-flat disk called the orbital plane. The orbital plane of an object orbiting another is the geometrical plane in which the orbit is embedded...
and in the direction of motion. For specific types of orbits, words such as "perihelion" (for Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
-centered orbits), "perigee" (for Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
-centered orbits), "periastron" (for orbits around stars) and so on may replace the word "periapsis". See apsis
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
for more information.
An argument of periapsis of 0° means that the orbiting body will be at its closest approach to the central body at the same moment that it crosses the plane of reference from South to North. An argument of periapsis of 90° means that the orbiting body will reach periapsis at its northmost distance from the plane of reference.
Adding the argument of periapsis to the longitude of the ascending node
Longitude of the ascending node
The longitude of the ascending node is one of the orbital elements used to specify the orbit of an object in space. It is the angle from a reference direction, called the origin of longitude, to the direction of the ascending node, measured in a reference plane...
gives the longitude of the periapsis
Longitude of the periapsis
In astrodynamics, the longitude of the periapsis of an orbiting body is the longitude at which the periapsis would occur if the body's inclination were zero. For motion of a planet around the sun, this position could be called longitude of perihelion...
. However, especially in discussions of binary stars and exoplanets, the terms "longitude of periapsis" or "longitude of periastron" are often used synonymously with "argument of periapsis".
Calculation
In astrodynamicsAstrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
the argument of periapsis ω can be calculated as follows:
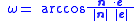
where:
-
is the vector pointing towards the ascending node (i.e. the z-component of 
is zero), -
is the eccentricity vectorEccentricity vectorIn astrodynamics, the eccentricity vector of a Kepler orbit is the vector pointing towards the periapsis having a magnitude equal to the orbit's scalar eccentricity. The magnitude is unitless. For Kepler orbits the eccentricity vector is a constant of motion...
(the vector pointing towards the periapsis).
In the case of equatorial orbits, though the argument is strictly undefined, it is often assumed that:
where:
is x-component of the eccentricity vector 
In the case of circular orbits it is often assumed that the periapsis is placed at the ascending node and therefore ω=0.