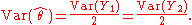Antithetic variates
Encyclopedia
The antithetic variates method is a variance reduction
technique used in Monte Carlo methods. Considering that the error reduction in the simulated signal (using Monte Carlo methods) has a square root
convergence
(standard deviation
of the solution), a very large number of sample
paths is required to obtain an accurate result.
to also take 
. The advantage of this technique is twofold: it reduces the number of normal samples to be taken to generate N paths, and it reduces the variance
of the sample paths, improving the accuracy.
Suppose that we would like to estimate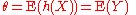
For that we have generated two samples
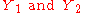
An unbiased estimate of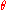
is given by
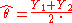
And
In the case where Y1 and Y2 are iid, covariance
self-cancels and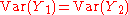
, therefore
The antithetic variates technique consists in this case of choosing the second sample in such a way that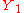
and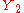 
are not iid anymore and 
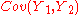is negative. As a result, 
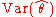is reduced and is smaller than the previous normal variance
.
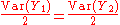along [0, 1], the first sample will be
, where, for any given i, 
is obtained from U(0, 1). The second sample is built from 
, where, for any given i: 
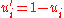. If the set 
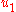is uniform along [0, 1], so are 
. Furthermore, covariance is negative, allowing for initial variance reduction.
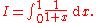
The exact result is
. This integral can be seen as the expected value of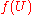 
, where
And U follows a uniform distribution
[0, 1].
The following table compares the classical Monte Carlo estimate (sample size: 2n, where n = 1500) to the antithetic variates estimate (sample size: n, completed with the transformed sample 1 − ui):
The use of the antithetic variates method to estimate the result shows an important variance reduction.
Variance reduction
In mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates that can be obtained for a given number of iterations. Every output random variable from the simulation is associated with a variance which...
technique used in Monte Carlo methods. Considering that the error reduction in the simulated signal (using Monte Carlo methods) has a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
convergence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
(standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the solution), a very large number of sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
paths is required to obtain an accurate result.
Underlying principle
The antithetic variates technique consists, for every sample path obtained, in taking its antithetic path — that is given a path to also take . The advantage of this technique is twofold: it reduces the number of normal samples to be taken to generate N paths, and it reduces the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the sample paths, improving the accuracy.
Suppose that we would like to estimate
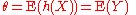
For that we have generated two samples
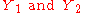
An unbiased estimate of
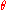is given by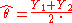And
In the case where Y1 and Y2 are iid, covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
self-cancels and
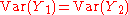, therefore
The antithetic variates technique consists in this case of choosing the second sample in such a way that
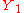and 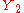are not iid anymore and 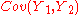is negative. As a result, 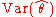is reduced and is smaller than the previous normal varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
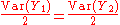.Example 1
If the law of the variable X follows a uniform distributionUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
along [0, 1], the first sample will be
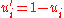, where, for any given i, is obtained from U(0, 1). The second sample is built from , where, for any given i: . If the set 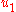is uniform along [0, 1], so are . Furthermore, covariance is negative, allowing for initial variance reduction.Example 2: integral calculation
We would like to estimate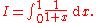The exact result is
. This integral can be seen as the expected value of 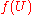, whereAnd U follows a uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
[0, 1].
The following table compares the classical Monte Carlo estimate (sample size: 2n, where n = 1500) to the antithetic variates estimate (sample size: n, completed with the transformed sample 1 − ui):
| Estimate | Variance | |
| Classical Estimate | 0,69365 | 0,02005 |
| Antithetic Variates | 0,69399 | 0,00063 |
The use of the antithetic variates method to estimate the result shows an important variance reduction.