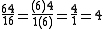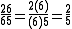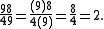Anomalous cancellation
Encyclopedia
An anomalous cancellation or accidental cancellation is a particular kind of arithmetic
procedural error that gives a numerically correct answer. An attempt is made to reduce
a fraction
by canceling individual digit
s in the numerator and denominator. This is not a legitimate operation, and does not in general give a correct answer, but in some rare cases the result is numerically the same as if a correct procedure had been applied.
Examples of anomalous cancellations which still produce the correct result include:
The article by Boas
analyzes two-digit cases in bases other than base 10, e.g., 32/13 = 2/1 is the only solution in base 4.
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
procedural error that gives a numerically correct answer. An attempt is made to reduce
Reduction (mathematics)
In mathematics, reduction refers to the rewriting of an expression into a simpler form. For example, the process of rewriting a fraction into one with the smallest whole-number denominator possible is called "reducing a fraction"...
a fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
by canceling individual digit
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
s in the numerator and denominator. This is not a legitimate operation, and does not in general give a correct answer, but in some rare cases the result is numerically the same as if a correct procedure had been applied.
Examples of anomalous cancellations which still produce the correct result include:
The article by Boas
Ralph P. Boas, Jr
Ralph Philip Boas, Jr was a mathematician, teacher, and journal editor. He wrote over 200 papers, mainly in the fields of real and complex analysis....
analyzes two-digit cases in bases other than base 10, e.g., 32/13 = 2/1 is the only solution in base 4.