Andrica's conjecture
Encyclopedia
Andrica's conjecture (named after Dorin Andrica) is a conjecture
regarding the gaps between prime number
s.
The conjecture states that the inequality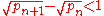
holds for all
, where 
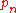is the nth prime number. If 
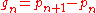denotes the nth prime gap, then Andrica's conjecture can also be rewritten as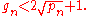
up to 1.3002 x 1016.
The discrete function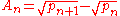
is plotted in the figures opposite. The high-water marks for 
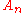occur for n = 1, 2, and 4, with A4 ≈ 0.670873..., with no larger value among the first 105 primes. Since the Andrica function decreases asymptotically as n increases, a prime gap of ever increasing size is needed to make the difference large as n becomes large. It therefore seems highly likely the conjecture is true, although this has not yet been proven.
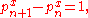
where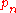
is the nth prime and n can be any positive integer.
The largest possible solution x is easily seen to occur for
, when xmax=1. The smallest solution x is conjectured to be xmin ≈ 0.567148... which occurs for n = 30.
This conjecture has also been stated as an inequality, the generalized Andrica conjecture:
for 
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
regarding the gaps between prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s.
The conjecture states that the inequality
holds for all
, where is the nth prime number. If 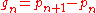denotes the nth prime gap, then Andrica's conjecture can also be rewritten as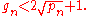Empirical evidence
Imran Ghory has used data on the largest prime gaps to confirm the conjecture for up to 1.3002 x 1016.The discrete function
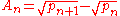is plotted in the figures opposite. The high-water marks for 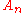occur for n = 1, 2, and 4, with A4 ≈ 0.670873..., with no larger value among the first 105 primes. Since the Andrica function decreases asymptotically as n increases, a prime gap of ever increasing size is needed to make the difference large as n becomes large. It therefore seems highly likely the conjecture is true, although this has not yet been proven.Generalizations
As a generalization of Andrica's conjecture, the following equation has been considered: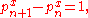where
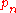is the nth prime and n can be any positive integer.The largest possible solution x is easily seen to occur for
, when xmax=1. The smallest solution x is conjectured to be xmin ≈ 0.567148... which occurs for n = 30.This conjecture has also been stated as an inequality, the generalized Andrica conjecture:
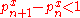for 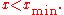External links
- Andrica's Conjecture at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
- Generalized Andrica conjecture at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...