
Alan M. Frieze
Encyclopedia
Alan M. Frieze is a professor
in the Department of Mathematical Sciences at Carnegie Mellon University
, Pittsburgh, United States
. He graduated from the University of Oxford
in 1966, and obtained his PhD from the University of London
in 1975. His research interests lie in combinatorics
, discrete optimization
and theoretical computer science
. Currently, he focuses on the probabilistic aspects of these areas; in particular, the study of the asymptotic properties of random graphs, the average case analysis of algorithms, and randomized algorithms. His recent work has included approximate counting and volume computation via random walks; finding edge disjoint paths in expander graphs, and exploring anti-Ramsey theory and the stability of routing algorithms.
(1) - polynomial time algorithm for approximating the volume of convex bodies
(2) - algorithmic version for Szemerédi regularity partition
Both these algorithms will be described briefly here.
is a joint work by Martin Dyer
, Alan Frieze and Ravindran Kannan
.
The main result of the paper is a randomized algorithm for finding an approximation to the volume of a convex body
approximation to the volume of a convex body  in
in  -dimensional Euclidean space by assume the existence of a membership oracle. The algorithm takes time bounded by a polynomial in
-dimensional Euclidean space by assume the existence of a membership oracle. The algorithm takes time bounded by a polynomial in  , the dimension of
, the dimension of  and
and 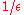 .
.
The algorithm is a sophisticated usage of the so-called Markov Chain Monte Carlo
(MCMC) method.
The basic scheme of the algorithm is a nearly uniform sampling from within by placing a grid consisting n-dimensional cubes and doing a random walk over these cubes. By using the theory of
by placing a grid consisting n-dimensional cubes and doing a random walk over these cubes. By using the theory of
rapidly mixing Markov chains
, they show that it takes a polynomial time for the random walk to settle down to being a nearly uniform distribution.
is a combined work by Alan Frieze and Ravindran Kannan
. They use two lemmas to derive the algorithmic version of the Szemerédi regularity lemma
to find an -regular partition.
-regular partition.
Lemma 1:
Fix k and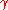 and let
and let 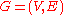 be a graph with
be a graph with  vertices. Let
vertices. Let 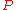 be an equitable partition of
be an equitable partition of  in classes
in classes 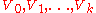 . Assume
. Assume  and
and 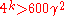 . Given proofs that more than
. Given proofs that more than 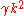 pairs
pairs 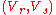 are not
are not 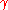 -regular, it is possible to find in O(n) time an equitable partition
-regular, it is possible to find in O(n) time an equitable partition 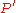 (which is a refinement of
(which is a refinement of 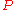 ) into
) into 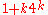 classes, with an exceptional class of cardinality at most
classes, with an exceptional class of cardinality at most  and such that
and such that 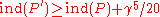
Lemma 2:
Let be a
be a 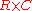 matrix with
matrix with  ,
, 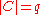 and
and  and
and 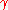 be a positive real.
be a positive real.
(a) If there exist ,
,  such that
such that 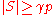 ,
,  and
and  then
then 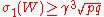
(b) If , then there exist
, then there exist  ,
,  such that
such that  ,
,  and
and 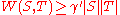 where
where 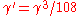 . Furthermore
. Furthermore 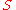 ,
,  can be constructed in polynomial time.
can be constructed in polynomial time.
These two lemmas are combined in the following algorithmic construction of the Szemerédi regularity lemma
.
[Step 1] Arbitrarily divide the vertices of into an equitable partition
into an equitable partition 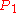 with classes
with classes 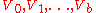 where
where 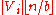 and hence
and hence 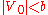 . denote
. denote 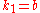 .
.
[Step 2] For every pair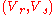 of
of 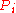 , compute
, compute  . If the pair
. If the pair 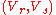 are not
are not  regular then by Lemma 2 we obtain a proof that they are not
regular then by Lemma 2 we obtain a proof that they are not 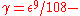 regular.
regular.
[Step 3] If there are at most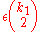 pairs that produce proofs of non
pairs that produce proofs of non 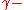 regularity that halt.
regularity that halt. 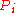 is
is  regular.
regular.
[Step 4] Apply Lemma 1 where ,
, 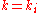 ,
, 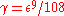 and obtain
and obtain 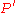 with
with 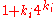 classes
classes
[Step 5] Let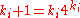 ,
, 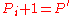 ,
, 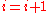 and go to Step 2.
and go to Step 2.
in Discrete Mathematics (Jointly with Martin Dyer and Ravi Kannan for the paper "A random polynomial time algorithm for approximating the volume of convex bodies" in the Journal of the Association for Computing Machinery) awarded by the Americam Mathematical Society and the Mathematical Programming Society.
In 1997 he was a Guggenheim Fellow
In 2000, he received the IBM Faculty Partnership Award
In 2006 he jointly received (with Michael Krivelevich) the Professor Pazy Memorial Research Award from the United States-Israel Binational Science Foundation.
In 2011 he was selected as a SIAM Fellow.
mix.
Professor
A professor is a scholarly teacher; the precise meaning of the term varies by country. Literally, professor derives from Latin as a "person who professes" being usually an expert in arts or sciences; a teacher of high rank...
in the Department of Mathematical Sciences at Carnegie Mellon University
Carnegie Mellon University
Carnegie Mellon University is a private research university in Pittsburgh, Pennsylvania, United States....
, Pittsburgh, United States
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
. He graduated from the University of Oxford
University of Oxford
The University of Oxford is a university located in Oxford, United Kingdom. It is the second-oldest surviving university in the world and the oldest in the English-speaking world. Although its exact date of foundation is unclear, there is evidence of teaching as far back as 1096...
in 1966, and obtained his PhD from the University of London
University of London
-20th century:Shortly after 6 Burlington Gardens was vacated, the University went through a period of rapid expansion. Bedford College, Royal Holloway and the London School of Economics all joined in 1900, Regent's Park College, which had affiliated in 1841 became an official divinity school of the...
in 1975. His research interests lie in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, discrete optimization
Discrete optimization
Discrete optimization is a branch of optimization in applied mathematics and computer science.As opposed to continuous optimization, the variables used in the mathematical program are restricted to assume only discrete values, such as the integers.Two notable branches of discrete optimization...
and theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
. Currently, he focuses on the probabilistic aspects of these areas; in particular, the study of the asymptotic properties of random graphs, the average case analysis of algorithms, and randomized algorithms. His recent work has included approximate counting and volume computation via random walks; finding edge disjoint paths in expander graphs, and exploring anti-Ramsey theory and the stability of routing algorithms.
Key contributions
Two key contributions made by Alan Frieze are:(1) - polynomial time algorithm for approximating the volume of convex bodies
(2) - algorithmic version for Szemerédi regularity partition
Both these algorithms will be described briefly here.
Polynomial time algorithm for approximating the volume of convex bodies
The paperis a joint work by Martin Dyer
Martin Dyer
Martin Edward Dyer is a professor in the School of Computing at the University of Leeds, Leeds, England. He graduated from the University of Leeds in 1967, obtained his MSc from Imperial College, University of London in 1968 and his PhD from the University of Leeds in 1979...
, Alan Frieze and Ravindran Kannan
Ravindran Kannan
Ravindran Kannan is currently a Principal Researcher at Microsoft Research India, where he leads the algorithms research group. He is also the first adjunct faculty of Computer Science and Automation Department of Indian Institute of Science. Before joining Microsoft, he was the William K. Lanman...
.
The main result of the paper is a randomized algorithm for finding an
 approximation to the volume of a convex body
approximation to the volume of a convex body  in
in  -dimensional Euclidean space by assume the existence of a membership oracle. The algorithm takes time bounded by a polynomial in
-dimensional Euclidean space by assume the existence of a membership oracle. The algorithm takes time bounded by a polynomial in  , the dimension of
, the dimension of  and
and 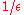 .
.The algorithm is a sophisticated usage of the so-called Markov Chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
(MCMC) method.
The basic scheme of the algorithm is a nearly uniform sampling from within
 by placing a grid consisting n-dimensional cubes and doing a random walk over these cubes. By using the theory of
by placing a grid consisting n-dimensional cubes and doing a random walk over these cubes. By using the theory ofrapidly mixing Markov chains
Markov chain mixing time
In probability theory, the mixing time of a Markov chain is the time until the Markov chain is "close" to its steady state distribution.More precisely, a fundamental result about Markov chains is that a finite state irreducible aperiodic chain has a unique stationary distribution π and,...
, they show that it takes a polynomial time for the random walk to settle down to being a nearly uniform distribution.
Algorithmic version for Szemerédi regularity partition
This paperis a combined work by Alan Frieze and Ravindran Kannan
Ravindran Kannan
Ravindran Kannan is currently a Principal Researcher at Microsoft Research India, where he leads the algorithms research group. He is also the first adjunct faculty of Computer Science and Automation Department of Indian Institute of Science. Before joining Microsoft, he was the William K. Lanman...
. They use two lemmas to derive the algorithmic version of the Szemerédi regularity lemma
Szemerédi regularity lemma
In mathematics, the Szemerédi regularity lemma states that every large enough graph can be divided into subsets of about the same size so that the edges between different subsets behave almost randomly. introduced a weaker version of this lemma, restricted to bipartite graphs, in order to prove ...
to find an
 -regular partition.
-regular partition.Lemma 1:
Fix k and
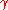 and let
and let 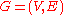 be a graph with
be a graph with  vertices. Let
vertices. Let 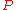 be an equitable partition of
be an equitable partition of  in classes
in classes 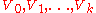 . Assume
. Assume  and
and 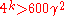 . Given proofs that more than
. Given proofs that more than 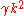 pairs
pairs 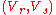 are not
are not 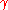 -regular, it is possible to find in O(n) time an equitable partition
-regular, it is possible to find in O(n) time an equitable partition 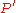 (which is a refinement of
(which is a refinement of 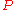 ) into
) into 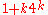 classes, with an exceptional class of cardinality at most
classes, with an exceptional class of cardinality at most  and such that
and such that 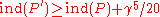
Lemma 2:
Let
 be a
be a 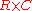 matrix with
matrix with  ,
, 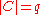 and
and  and
and 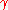 be a positive real.
be a positive real.(a) If there exist
 ,
,  such that
such that 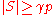 ,
,  and
and  then
then 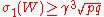
(b) If
 , then there exist
, then there exist  ,
,  such that
such that  ,
,  and
and 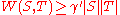 where
where 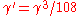 . Furthermore
. Furthermore 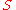 ,
,  can be constructed in polynomial time.
can be constructed in polynomial time.These two lemmas are combined in the following algorithmic construction of the Szemerédi regularity lemma
Szemerédi regularity lemma
In mathematics, the Szemerédi regularity lemma states that every large enough graph can be divided into subsets of about the same size so that the edges between different subsets behave almost randomly. introduced a weaker version of this lemma, restricted to bipartite graphs, in order to prove ...
.
[Step 1] Arbitrarily divide the vertices of
 into an equitable partition
into an equitable partition 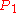 with classes
with classes 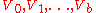 where
where 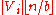 and hence
and hence 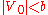 . denote
. denote 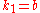 .
.[Step 2] For every pair
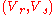 of
of 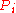 , compute
, compute  . If the pair
. If the pair 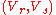 are not
are not  regular then by Lemma 2 we obtain a proof that they are not
regular then by Lemma 2 we obtain a proof that they are not 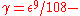 regular.
regular.[Step 3] If there are at most
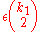 pairs that produce proofs of non
pairs that produce proofs of non 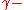 regularity that halt.
regularity that halt. 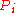 is
is  regular.
regular.[Step 4] Apply Lemma 1 where
 ,
, 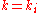 ,
, 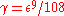 and obtain
and obtain 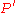 with
with 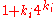 classes
classes[Step 5] Let
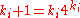 ,
, 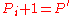 ,
, 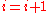 and go to Step 2.
and go to Step 2.Awards and honors
In 1991, Dr. Frieze received the Fulkerson PrizeFulkerson Prize
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Programming Society and the American Mathematical Society . Up to three awards of $1500 each are presented at each International Symposium of the MPS...
in Discrete Mathematics (Jointly with Martin Dyer and Ravi Kannan for the paper "A random polynomial time algorithm for approximating the volume of convex bodies" in the Journal of the Association for Computing Machinery) awarded by the Americam Mathematical Society and the Mathematical Programming Society.
In 1997 he was a Guggenheim Fellow
In 2000, he received the IBM Faculty Partnership Award
In 2006 he jointly received (with Michael Krivelevich) the Professor Pazy Memorial Research Award from the United States-Israel Binational Science Foundation.
In 2011 he was selected as a SIAM Fellow.
Personal
Dr. Alan Frieze is married to Carol Frieze, Director, Women@SCS, and Co-Director, Women@IT, School of Computer Science, Carnegie Mellon University. They have two children, son Adam (currently teaching in England) and daughter Nancy, son-in-law Joe, and grandbabies Maisie, Molly and Gracie. The family also includes Max, a RottweilerRottweiler
The Rottweiler is a medium to large size breed of domestic dog that originated in Rottweil, Germany. The dogs were known as "Rottweil butchers' dogs" because they were used to herd livestock and pull carts laden with butchered meat and other products to market...
mix.

