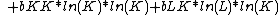A list of production functions
Encyclopedia
The production functions listed below, and their properties are shown for the case of two factors of production, capital (K), and labor (L), mostly for heuristic purposes. These functions and their properties are easily generalizable to include additional factors of production (like land, natural resources, entrepreneurship, etc.)
A production function
can also be seen as the dynamics of national output/national income. This list is to collect production functions & the dynamics of national output/income that have been used in literature & textbooks.
. The mathematical definition is:
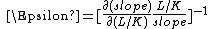
where "slope" denotes the slope of the isoquant, given by:
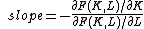
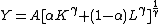, with 
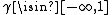which includes the special cases of:
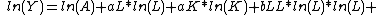
The PAR production functions have such flexible limiting properties which are lacking in the CES technology. The Cobb-Douglas production function (a=0) as well as the Leontief production function (a→∞) are special cases of the PAR technology. The general form of the PAR production function is as follows:
Y = A*[c*(D^\−a −L^\−a)/((D/L)^\-a*c-1)]^\−(1/a) (a ≠ 0)(c ≠ 0)(D ≠ L)
= A**[c*(D^\−a −L^\−a)/(-a*ln(D/L))]^\−(1/a) (a ≠ 0)(c = 0)(D ≠ L)
= A* D^\((1-c)/2)* L^\((1+c)/2) (a = 0)(-1≤c≤1)(D ≠ L)
= A*D (D = L)
If a=-1, then
Y = A*c*(D-L)/[( D/L)^\c-1] (a = -1)(c ≠ 0)(D ≠ L)
= A*(D-L)/[ln(D/L)] (a = -1)(c = 0)(D ≠ L)
In the above equation, Y is the physical output of production, D is input 1, L is input 2, “c” is the distribution limit parameter and “a” is the substitution parameter. Features of PAR technology are thoroughly examined by Tenhunen (1990).
Lauri Tenhunen, The CES and Par Production Techniques, Income Distribution, and the Neoclassical Theory of Production. Acta Universitatis Tamperensis ser A vol 290. Tampere 1990. http://acta.uta.fi/pdf/978-951-44-8581-7.pdf
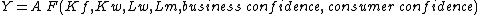while 
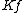is the fixed capital, 
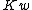is the working capital, 
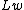is the working labor, 
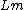is the management labor.
A production function
Production function
In microeconomics and macroeconomics, a production function is a function that specifies the output of a firm, an industry, or an entire economy for all combinations of inputs...
can also be seen as the dynamics of national output/national income. This list is to collect production functions & the dynamics of national output/income that have been used in literature & textbooks.
Technology
There are three common ways to incorporate technology (or the efficiency with which factors of production are used) into a production function:- Hicks-neutral technologyHicks-neutral technical changeA Hicks-neutral technical change is a change in the production function of a business or industry which satifies certain economic neutrality conditions. The concept of Hicks neutrality was first put forth in 1932 by John Hicks in his book The Theory of Wages...
, or "factor augmenting":
- Harrod-neutral technology, or "labor augmenting":
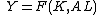
- Solow-neutral technology, or "capital augmenting":
Elasticity of substitution
The elasticity of substitution between factors of production is a measure of how easily one factor can be substituted for another. With two factors of production, say, K and L, it is a measure of the curvature of a production isoquantIsoquant
In economics, an isoquant is a contour line drawn through the set of points at which the same quantity of output is produced while changing the quantities of two or more inputs...
. The mathematical definition is:
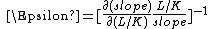
where "slope" denotes the slope of the isoquant, given by:
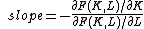
Return to Scale
- Increasing return to scale.
- Constant return to scale.
- Decreasing returns to scale.
Some Famous forms
- Constant elasticity of substitutionElasticity of substitutionElasticity of substitution is the elasticity of the ratio of two inputs to a production function with respect to the ratio of their marginal products . It measures the curvature of an isoquant and thus, the substitutability between inputs , i.e...
(CES) function:
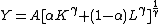, with 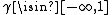which includes the special cases of:-
-
- Linear production (or perfect substitutes)
-
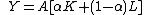when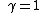 
- Cobb-DouglasCobb-DouglasIn economics, the Cobb–Douglas functional form of production functions is widely used to represent the relationship of an output to inputs. Similar functions were originally used by Knut Wicksell , while the Cobb-Douglas form was developed and tested against statistical evidence by Charles Cobb and...
(or imperfect complements)
-
when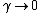 
- Leontief production functionLeontief production functionIn economics, the Leontief production function or fixed proportions production function is a production function that implies the factors of production will be used in fixed proportions, as there is no substitutability between factors...
(or perfect complements)
-
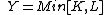when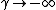 
-
- Translog (generalization of the above)
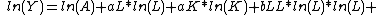
- The PAR production technology
The PAR production functions have such flexible limiting properties which are lacking in the CES technology. The Cobb-Douglas production function (a=0) as well as the Leontief production function (a→∞) are special cases of the PAR technology. The general form of the PAR production function is as follows:
Y = A*[c*(D^\−a −L^\−a)/((D/L)^\-a*c-1)]^\−(1/a) (a ≠ 0)(c ≠ 0)(D ≠ L)
= A**[c*(D^\−a −L^\−a)/(-a*ln(D/L))]^\−(1/a) (a ≠ 0)(c = 0)(D ≠ L)
= A* D^\((1-c)/2)* L^\((1+c)/2) (a = 0)(-1≤c≤1)(D ≠ L)
= A*D (D = L)
If a=-1, then
Y = A*c*(D-L)/[( D/L)^\c-1] (a = -1)(c ≠ 0)(D ≠ L)
= A*(D-L)/[ln(D/L)] (a = -1)(c = 0)(D ≠ L)
In the above equation, Y is the physical output of production, D is input 1, L is input 2, “c” is the distribution limit parameter and “a” is the substitution parameter. Features of PAR technology are thoroughly examined by Tenhunen (1990).
Lauri Tenhunen, The CES and Par Production Techniques, Income Distribution, and the Neoclassical Theory of Production. Acta Universitatis Tamperensis ser A vol 290. Tampere 1990. http://acta.uta.fi/pdf/978-951-44-8581-7.pdf
Factors
Some authors also propose "indirect" production function. Production function can be assumed to have more factors in play, and with some factors refined. For instanc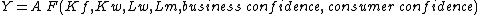e, while 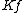is the fixed capital, 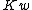is the working capital, 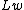is the working labor, 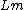is the management labor.