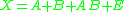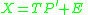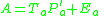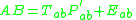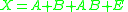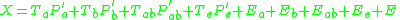ANOVA-simultaneous component analysis
Encyclopedia
ASCA, ANOVA-SCA, or analysis of variance – simultaneous component analysis is a method that partitions variation and enables interpretation of these partitions by SCA, a method that is similar to PCA
. This method is a multi or even megavariate extension of ANOVA. The variation partitioning is similar to Analysis of variance (ANOVA). Each partition matches all variation induced by an effect or factor, usually a treatment regime or experimental condition. The calculated effect partitions are called effect estimates. Because even the effect estimates are multivariate, interpretation of these effects estimates is not intuitive. By applying SCA on the effect estimates one gets a simple interpretable result.
In case of more than one effect this method estimates the effects in such a way that the different effects are not correlated.
and singularity. Because of this, most traditional multivariate statistical methods cannot be applied.
Let X be a matrix that holds the data. X is mean centered, thus having zero mean columns. Let A and B denote the main effects and AB the interaction of these effects. Two main effects in a biological experiment can be time (A) and pH
(B), and these two effects may interact. In designing such experiments one controls the main effects to several (at least two) levels. The different levels of an effect can be referred to as A1, A2, A3 and A4, representing 2, 3, 4, 5 hours from the start of the experiment. The same thing holds for effect B, for example, pH 6, pH 7 and pH 8 can be considered effect levels.
A and B are required to be balanced if the effect estimates need to be orthogonal and the partitioning unique. Matrix E holds the information that is not assigned to any effect. The partitioning gives the following notation:
After completing the level estimates for the effect, perform an SCA. The scores of this SCA are the sample deviations for the effect, the important variables of this effect are in the weights of the SCA loading vector.
, but is semantically different in that it models different objects or subjects at the same time.
The standard notation for a SCA – and PCA – model is:
where X is the data, T are the component scores and P are the component loadings. E is the residual or error matrix. Because ASCA models the variation partitions by SCA, the model for effect estimates looks like this:
Note that every partition has its own error matrix. However, algebra dictates that in a balanced mean centered data set every two level system is of rank one. This results in zero errors, since any rank 1 matrix can be written as the product of a single component score and loading vector.
The full ASCA model with two effects and interaction including the SCA looks like this:
Decomposition:
Principal components analysis
Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
. This method is a multi or even megavariate extension of ANOVA. The variation partitioning is similar to Analysis of variance (ANOVA). Each partition matches all variation induced by an effect or factor, usually a treatment regime or experimental condition. The calculated effect partitions are called effect estimates. Because even the effect estimates are multivariate, interpretation of these effects estimates is not intuitive. By applying SCA on the effect estimates one gets a simple interpretable result.
In case of more than one effect this method estimates the effects in such a way that the different effects are not correlated.
Details
Many research areas see increasingly large numbers of variables in only few samples. The low sample to variable ratio creates problems known as multicollinearityMulticollinearity
Multicollinearity is a statistical phenomenon in which two or more predictor variables in a multiple regression model are highly correlated. In this situation the coefficient estimates may change erratically in response to small changes in the model or the data...
and singularity. Because of this, most traditional multivariate statistical methods cannot be applied.
ASCA algorithm
This section details how to calculate the ASCA model on a case of two main effects with one interaction effect. It is easy to extend the declared rationale to more main effects and more interaction effects. If the first effect is time and the second effect is dosage, only the interaction between time and dosage exist. We assume there are four time points and three dosage levels.Let X be a matrix that holds the data. X is mean centered, thus having zero mean columns. Let A and B denote the main effects and AB the interaction of these effects. Two main effects in a biological experiment can be time (A) and pH
PH
In chemistry, pH is a measure of the acidity or basicity of an aqueous solution. Pure water is said to be neutral, with a pH close to 7.0 at . Solutions with a pH less than 7 are said to be acidic and solutions with a pH greater than 7 are basic or alkaline...
(B), and these two effects may interact. In designing such experiments one controls the main effects to several (at least two) levels. The different levels of an effect can be referred to as A1, A2, A3 and A4, representing 2, 3, 4, 5 hours from the start of the experiment. The same thing holds for effect B, for example, pH 6, pH 7 and pH 8 can be considered effect levels.
A and B are required to be balanced if the effect estimates need to be orthogonal and the partitioning unique. Matrix E holds the information that is not assigned to any effect. The partitioning gives the following notation:
Calculating main effect estimate A (or B)
Find all rows that correspond to effect A level 1 and averages these rows. The result is a vector. Repeat this for the other effect levels. Make a new matrix of the same size of X and place the calculated averages in the matching rows. That is, give all rows that match effect (i.e.) A level 1 the average of effect A level 1.After completing the level estimates for the effect, perform an SCA. The scores of this SCA are the sample deviations for the effect, the important variables of this effect are in the weights of the SCA loading vector.
Calculating interaction effect estimate AB
Estimating the interaction effect is similar to estimating main effects. The difference is that for interaction estimates the rows that match effect A level 1 are combined with the effect B level 1 and all combinations of effects and levels are cycled through. In our example setting, with four time point and three dosage levels there are 12 interaction sets {A1-B1, A1B2, A2B1, A2B2 and so on}. It is important to deflate (remove) the main effects before estimating the interaction effect.SCA on partitions A, B and AB
Simultaneous component analysis is mathematically identical to PCAPrincipal components analysis
Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
, but is semantically different in that it models different objects or subjects at the same time.
The standard notation for a SCA – and PCA – model is:
where X is the data, T are the component scores and P are the component loadings. E is the residual or error matrix. Because ASCA models the variation partitions by SCA, the model for effect estimates looks like this:
Note that every partition has its own error matrix. However, algebra dictates that in a balanced mean centered data set every two level system is of rank one. This results in zero errors, since any rank 1 matrix can be written as the product of a single component score and loading vector.
The full ASCA model with two effects and interaction including the SCA looks like this:
Decomposition: