
15 theorem
Encyclopedia
The 15 theorem of John H. Conway and W. A. Schneeberger (Conway–Schneeberger Fifteen Theorem), proved in 1993, states that if an integral quadratic form
with integer matrix
represents all positive integers up to 15
, then it represents all positive integers. (All quadratic forms in this article are implicitly assumed to be positive definite.) The proof was complicated, and was never published. Manjul Bhargava
found a much simpler proof which was published in 2000.
This result is the best possible, as there are such forms as, for example,
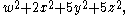
that represent all positive integers other than 15.
A quadratic form representing all positive integers is sometimes called universal. For example,
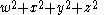
is universal because every positive integer can be written as a sum of 4 squares, by Lagrange's four-square theorem
. By the 15 theorem, to verify this it is sufficient to check that every positive integer up to 15 is a sum of 4 squares. (This does not give an alternative proof of Lagrange's theorem, because Lagrange's theorem is used in the proof of the 15 theorem.)
A more precise version of the 15 theorem says that if an integral quadratic form with integral matrix represents the numbers 1, 2, 3, 5, 6, 7, 10, 14, 15 then it represents all positive integers. Moreover, for each of these 9 numbers, there is such a quadratic form representing all positive integers except for this number.
There are two different notions of integrality for integral quadratic forms: it can be called integral if its associated symmetric matrix is integral ("integral matrix"), or if all its coefficients are integral ("integer valued"). For example,
x2 + xy + y2 is integer valued but does not have integral matrix.
In 2005 Manjul Bhargava
and Jonathan P. Hanke announced a proof of Conway's conjecture that a similar theorem
holds for integer valued integral quadratic forms, with the constant 15 replaced by 290
. The proof is forthcoming in Inventiones Mathematicae
.
A more precise version states that if an integer valued integral quadratic form represents all the numbers 1, 2, 3, 5, 6, 7, 10, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 34, 35, 37, 42, 58, 93, 110, 145, 203, 290 then it represents all positive integers, and for each of these 29 numbers there is such a quadratic form representing all positive integers with the exception of this one number.
Bhargava has found analogous criteria for an integral quadratic form to represent all primes (the set {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 67, 73} ) and for such a quadratic form to represent all positive odd integers (the set {1, 3, 5, 7, 11, 15, 33} ).
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
with integer matrix
Integer matrix
In mathematics, an integer matrix is a matrix whose entries are all integers. Examples include binary matrices, the zero matrix, the unit matrix, and the adjacency matrices used in graph theory, amongst many others...
represents all positive integers up to 15
15 (number)
15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name....
, then it represents all positive integers. (All quadratic forms in this article are implicitly assumed to be positive definite.) The proof was complicated, and was never published. Manjul Bhargava
Manjul Bhargava
Manjul Bhargava is a Canadian-American mathematician of Indian origin. He is the R. Brandon Fradd Professor of Mathematics at Princeton University...
found a much simpler proof which was published in 2000.
This result is the best possible, as there are such forms as, for example,
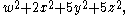
that represent all positive integers other than 15.
A quadratic form representing all positive integers is sometimes called universal. For example,
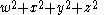
is universal because every positive integer can be written as a sum of 4 squares, by Lagrange's four-square theorem
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
. By the 15 theorem, to verify this it is sufficient to check that every positive integer up to 15 is a sum of 4 squares. (This does not give an alternative proof of Lagrange's theorem, because Lagrange's theorem is used in the proof of the 15 theorem.)
A more precise version of the 15 theorem says that if an integral quadratic form with integral matrix represents the numbers 1, 2, 3, 5, 6, 7, 10, 14, 15 then it represents all positive integers. Moreover, for each of these 9 numbers, there is such a quadratic form representing all positive integers except for this number.
There are two different notions of integrality for integral quadratic forms: it can be called integral if its associated symmetric matrix is integral ("integral matrix"), or if all its coefficients are integral ("integer valued"). For example,
x2 + xy + y2 is integer valued but does not have integral matrix.
In 2005 Manjul Bhargava
Manjul Bhargava
Manjul Bhargava is a Canadian-American mathematician of Indian origin. He is the R. Brandon Fradd Professor of Mathematics at Princeton University...
and Jonathan P. Hanke announced a proof of Conway's conjecture that a similar theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
holds for integer valued integral quadratic forms, with the constant 15 replaced by 290
290 (number)
290 is the natural number after 289 and before 291.-In mathematics:The product of three primes, 290 is a sphenic number, and the sum of four consecutive primes . The sum of the squares of the divisors of 17 is 290...
. The proof is forthcoming in Inventiones Mathematicae
Inventiones Mathematicae
Inventiones Mathematicae, often just referred to as Inventiones, is a mathematical journal published monthly by Springer Verlag. It was founded in 1966.-Editors:...
.
A more precise version states that if an integer valued integral quadratic form represents all the numbers 1, 2, 3, 5, 6, 7, 10, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 34, 35, 37, 42, 58, 93, 110, 145, 203, 290 then it represents all positive integers, and for each of these 29 numbers there is such a quadratic form representing all positive integers with the exception of this one number.
Bhargava has found analogous criteria for an integral quadratic form to represent all primes (the set {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 67, 73} ) and for such a quadratic form to represent all positive odd integers (the set {1, 3, 5, 7, 11, 15, 33} ).

