(p,q) shuffle
Encyclopedia
Let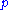 
and 
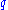be positive natural numbers. Further, let 
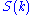be the set of permutation
s of the numbers
. A permutation 
in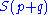 
is a (p,q)shuffle if
,
.
The set of all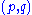
shuffles is denoted by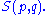 
It is clear that
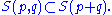
Since a
shuffle is completely determined by how the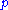 
first elements are mapped, the cardinality of 
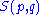is
The wedge product of a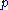
-form and a 
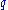-form can be defined as a sum over 
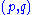shuffles.
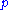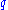and be positive natural numbers. Further, let 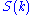be the set of permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of the numbers
. A permutation in 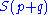is a (p,q)shuffle if,. The set of all
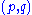shuffles is denoted by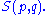 It is clear that
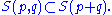
Since a
shuffle is completely determined by how the 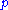first elements are mapped, the cardinality of 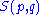isThe wedge product of a
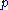-form and a 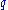-form can be defined as a sum over 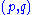shuffles.