
Xiaolin Wu's line algorithm
Encyclopedia
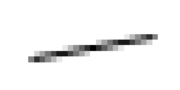
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for line antialiasing, which was presented in the article An Efficient Antialiasing Technique in the July 1991 issue of Computer Graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, as well as in the article Fast Antialiasing in the June 1992 issue of Dr. Dobb's Journal
Dr. Dobb's Journal
Dr. Dobb's Journal was a monthly journal published in the United States by CMP Technology. It covered topics aimed at computer programmers. DDJ was the first regular periodical focused on microcomputer software, rather than hardware. It later became a monthly section within the periodical...
.
Bresenham's algorithm
Bresenham's line algorithm
The Bresenham line algorithm is an algorithm which determines which points in an n-dimensional raster should be plotted in order to form a close approximation to a straight line between two given points...
draws lines extremely quickly, but it does not perform anti-aliasing. In addition, it cannot handle the case where the line endpoints do not lie exactly on integer points of the pixel grid. A naïve approach to anti-aliasing the line would take an extremely long time, but Wu's algorithm is quite fast (it is still slower than Bresenham's, though). The basis of the algorithm is to draw pairs of pixels straddling the line, coloured according to proximity. Pixels at the line ends are handled separately. Lines less than one pixel long should be handled as a special case.
An extension to the algorithm for circle drawing was presented by Xiaolin Wu in the book Graphics Gems II. Just like the line drawing algorithm is a replacement for Bresenham's line drawing algorithm, the circle drawing algorithm is a replacement for Bresenham's circle drawing algorithm.
function plot(x, y, c) is
plot the pixel at (x, y) with brightness c (where 0 ≤ c ≤ 1)
function ipart(x) is
return integer part of x
function round(x) is
return ipart(x + 0.5)
function fpart(x) is
return fractional part of x
function rfpart(x) is
return 1 - fpart(x)
function drawLine(x1,y1,x2,y2) is
dx = x2 - x1
dy = y2 - y1
if abs(dx) < abs(dy) then
swap x1, y1
swap x2, y2
swap dx, dy
end if
if x2 < x1
swap x1, x2
swap y1, y2
end if
gradient = dy / dx
// handle first endpoint
xend = round(x1)
yend = y1 + gradient * (xend - x1)
xgap = rfpart(x1 + 0.5)
xpxl1 = xend // this will be used in the main loop
ypxl1 = ipart(yend)
plot(xpxl1, ypxl1, rfpart(yend) * xgap)
plot(xpxl1, ypxl1 + 1, fpart(yend) * xgap)
intery = yend + gradient // first y-intersection for the main loop
// handle second endpoint
xend = round (x2)
yend = y2 + gradient * (xend - x2)
xgap = fpart(x2 + 0.5)
xpxl2 = xend // this will be used in the main loop
ypxl2 = ipart (yend)
plot (xpxl2, ypxl2, rfpart (yend) * xgap)
plot (xpxl2, ypxl2 + 1, fpart (yend) * xgap)
// main loop
for x from xpxl1 + 1 to xpxl2 - 1 do
plot (x, ipart (intery), rfpart (intery))
plot (x, ipart (intery) + 1, fpart (intery))
intery = intery + gradient
end function
Note: If at the beginning of the routine abs(dx) < abs(dy) is true, then all plotting should be done with x and y reversed.

