
Watson's lemma
Encyclopedia
In mathematics, Watson's lemma, proved by G. N. Watson
(1918, p. 133), has significant application within the theory on the asymptotic behavior of integral
s.
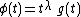 , where
, where 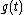 has an infinite number of derivatives in the neighborhood of
has an infinite number of derivatives in the neighborhood of 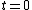 , with
, with 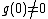 , and
, and 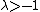 .
.
Suppose, in addition, that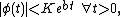
where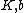 are independent of
are independent of  .
.
Then, it is true that for all positive that
that
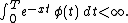
and the following asymptotic equivalence holds: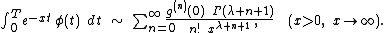
Proof: See, for instance, for the original proof or for a more recent development.
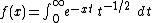
for large values of , that is when
, that is when 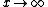 .
.
Solution: By direct application of Watson's lemma, with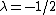 and
and 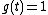 ,
,
so that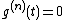 for
for 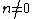 . It is easy to see that:
. It is easy to see that:
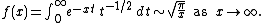
This development used the fact that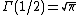 , a known property of the Gamma function
, a known property of the Gamma function
.
G. N. Watson
Neville Watson was an English mathematician, a noted master in the application of complex analysis to the theory of special functions. His collaboration on the 1915 second edition of E. T. Whittaker's A Course of Modern Analysis produced the classic “Whittaker & Watson” text...
(1918, p. 133), has significant application within the theory on the asymptotic behavior of integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s.
Statement of the lemma
Assume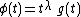 , where
, where 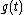 has an infinite number of derivatives in the neighborhood of
has an infinite number of derivatives in the neighborhood of 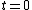 , with
, with 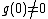 , and
, and 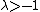 .
.Suppose, in addition, that
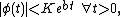
where
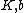 are independent of
are independent of  .
.Then, it is true that for all positive
 that
that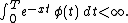
and the following asymptotic equivalence holds:
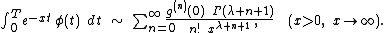
Proof: See, for instance, for the original proof or for a more recent development.
Example
Find a simple asymptotic approximation for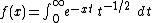
for large values of
 , that is when
, that is when 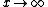 .
.Solution: By direct application of Watson's lemma, with
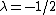 and
and 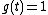 ,
,so that
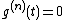 for
for 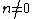 . It is easy to see that:
. It is easy to see that: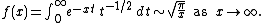
This development used the fact that
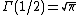 , a known property of the Gamma function
, a known property of the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.

