Vinogradov's theorem
Encyclopedia
In number theory
, Vinogradov's theorem implies that any sufficiently large odd integer
can be written as a sum of three prime number
s. It is a weaker form of Goldbach's conjecture
, which would imply the existence of such a representation for all odd integers greater than five. It is named after Ivan Matveyevich Vinogradov
who proved it in the 1930s. The full statement of Vinogradov's theorem gives asymptotic bounds
on the number of representations of an odd integer as a sum of three primes.
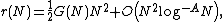
where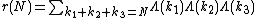
,
using the von Mangoldt function
, and
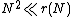for all sufficiently large N. By showing that the contribution made to r(N) by proper prime powers is 
, one sees that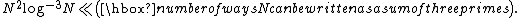
This means in particular that any sufficiently large odd integer can be written as a sum of three primes, thus showing Goldbach's weak conjecture
for all but finitely many cases.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Vinogradov's theorem implies that any sufficiently large odd integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
can be written as a sum of three prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. It is a weaker form of Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
, which would imply the existence of such a representation for all odd integers greater than five. It is named after Ivan Matveyevich Vinogradov
Ivan Matveyevich Vinogradov
Ivan Matveevich Vinogradov was a Soviet mathematician, who was one of the creators of modern analytic number theory, and also a dominant figure in mathematics in the USSR. He was born in the Velikiye Luki district, Pskov Oblast. He graduated from the University of St...
who proved it in the 1930s. The full statement of Vinogradov's theorem gives asymptotic bounds
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
on the number of representations of an odd integer as a sum of three primes.
Statement of Vinogradov's theorem
Let A be a positive real number. Then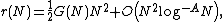where
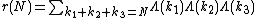,using the von Mangoldt function
Von Mangoldt function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
, andA consequence
If N is odd, then G(N) is roughly 1, hence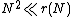 for all sufficiently large N. By showing that the contribution made to r(N) by proper prime powers is , one sees that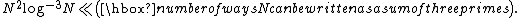This means in particular that any sufficiently large odd integer can be written as a sum of three primes, thus showing Goldbach's weak conjecture
Goldbach's weak conjecture
In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states that:...
for all but finitely many cases.