Varignon's theorem is a statement in Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

 by Pierre Varignon

Pierre Varignon

Pierre Varignon was a French mathematician. He was educated at the Jesuit College and the University in Caen, where he received his M.A. in 1682. He took Holy Orders the following year....

 that was first published in 1731. It deals with the construction of a particular parallelogram

Parallelogram

In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

 (Varignon parallelogram) from an arbitrary quadrangle

Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

.

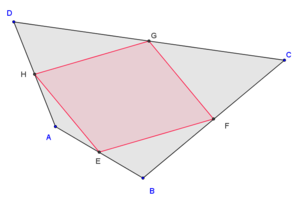
The midpoints of the sides of an arbitrary quadrangle form a parallelogram. If the quadrangle is convex or reentrant, i.e. not a crossing quadrangle, then the area of the parallelogram is half as big as the area of the quadrangle.

If one introduces the concept of oriented areas for n-gons

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

, then the area equality above holds for crossed quadrangles as well.

The Varignon parallelogram exists even for a skew quadrilateral, and is planar whether or not the quadrilateral is planar.

Proof

Varignon's theorem is easily proved as a theorem of affine geometry organized as linear algebra with the linear combinations restricted to coefficients summing to 1, also called affine or barycentric coordinates

Barycentric coordinates (mathematics)

In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...

. The proof applies even to skew quadrilaterals in spaces of any dimension.

Any three points E, F, G are completed to a parallelogram (lying in the plane containing E, F, and G) by taking its fourth vertex to be E − F + G. In the construction of the Varignon parallelogram this is the point (A + B)/2 − (B + C)/2 + (C + D)/2 = (A + D)/2. But this is the point H in the figure, whence EFGH forms a parallelogram.

In short, the centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

of the four points A, B, C, D is the midpoint of each of the two diagonals EG and FH of EFGH, showing that the midpoints coincide.

convex quadrangle	reentrant quadrangle	crossed quadrangle

External links

• Varignon Parallelogram in Compendium Geometry