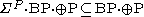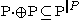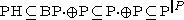Toda's theorem
Encyclopedia
Toda's theorem was proven by Seinosuke Toda
in his paper "PP is as Hard as the Polynomial-Time Hierarchy" (1991) and was given the 1998 Gödel Prize
. The theorem states that the entire polynomial hierarchy PH is contained in PPP; this implies a closely related statement, that PH is contained in P#P. #P
is the problem of exactly counting the number of solutions to a polynomially-verifiable question (that is, to a question in NP
), while loosely speaking, PP
is the problem of giving an answer which is correct at least half the time. The class P#P consists of all the problems which can be solved in polynomial time if you have access to instantaneous answers to any counting problem in #P (polynomial time relative to a #P oracle). Thus Toda's theorem implies that for any problem in the polynomial hierarchy there is a deterministic polynomial-time Turing reduction to a counting problem.
The proof is broken into two parts.
Together, the two parts imply
Seinosuke Toda
is a computer scientist working at the Nihon University in Tokyo. He was a recipient of the 1998 Gödel Prize for proving Toda's theorem.-External links:* at the Nihon University....
in his paper "PP is as Hard as the Polynomial-Time Hierarchy" (1991) and was given the 1998 Gödel Prize
Gödel Prize
The Gödel Prize is a prize for outstanding papers in theoretical computer science, named after Kurt Gödel and awarded jointly by the European Association for Theoretical Computer Science and the Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory .The...
. The theorem states that the entire polynomial hierarchy PH is contained in PPP; this implies a closely related statement, that PH is contained in P#P. #P
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
is the problem of exactly counting the number of solutions to a polynomially-verifiable question (that is, to a question in NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
), while loosely speaking, PP
PP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time...
is the problem of giving an answer which is correct at least half the time. The class P#P consists of all the problems which can be solved in polynomial time if you have access to instantaneous answers to any counting problem in #P (polynomial time relative to a #P oracle). Thus Toda's theorem implies that for any problem in the polynomial hierarchy there is a deterministic polynomial-time Turing reduction to a counting problem.
The proof is broken into two parts.
- First, it is established that
- The proof uses a variation of Valiant-Vazirani theoremValiant-Vazirani theoremThe Valiant–Vazirani theorem is a theorem in computational complexity theory. It was proven by Leslie Valiant and Vijay Vazirani in their paper titled "NP is as easy as detecting unique solutions" published in 1986...
. Because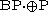
contains 
and is closed under complement, it follows by induction that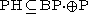 
.
- Second, it is established that
Together, the two parts imply
