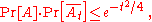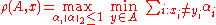Talagrand's concentration inequality
Encyclopedia
In probability theory
, Talagrand's concentration inequality, is an isoperimetric-type inequality for product probability space
s. It was first proved by the French mathematician Michel Talagrand
. The inequality is one of the manifestations of the concentration of measure
phenomenon.
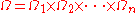is a product space endowed with a product probability measure
and
is a subset in this space, then for any
where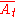
is the complement of At where this is defined by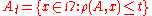
and where
is Talagrand's convex distance defined as
whe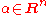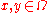re
, 
are 
-dimensional vectors with entries
respectively and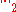 
is the 2-norm.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Talagrand's concentration inequality, is an isoperimetric-type inequality for product probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
s. It was first proved by the French mathematician Michel Talagrand
Michel Talagrand
Michel Pierre Talagrand is a French mathematician. Docteur ès sciences since 1977, he has been, since 1985, Directeur de Recherches at CNRS and a member of the Functional Analysis Team of the Institut de Mathématique of Paris...
. The inequality is one of the manifestations of the concentration of measure
Concentration of measure
In mathematics, concentration of measure is a principle that is applied in measure theory, probability and combinatorics, and has consequences for other fields such as Banach space theory. Informally, it states that "A random variable that depends in a Lipschitz way on many independent variables ...
phenomenon.
Statement
The inequality states that if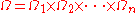 is a product space endowed with a product probability measureProduct measure
In mathematics, given two measurable spaces and measures on them, one can obtain the product measurable space and the product measure on that space...
and
is a subset in this space, then for any
where
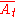is the complement of At where this is defined by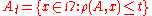and where
is Talagrand's convex distance defined as
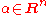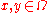where
, are -dimensional vectors with entries respectively and 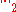is the 2-norm.