Saint-Venant's compatibility condition
Encyclopedia
In the mathematical theory of elasticity the strain 
is related to a displacement field 
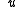by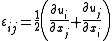
Barré de Saint-Venant
derived the compatibility condition for an arbitrary symmetric second rank tensor field to be of this form, this has now been generalized to higher rank symmetric tensor fields.
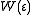defined by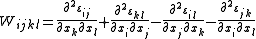
The result that, on a simply connected domain W=0 implies that strain is the symmetric derivative of some vector field, was first described by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami
in 1886. For non-simply connected domains there are finite dimensional spaces of symmetric tensors with vanishing Saint-Venant's tensor that are not the symmetric derivative of a vector field. The situation is analogous to de Rham cohomology
Due to the symmetry conditions
there are only six (in the three dimensional case) distinct components of 
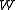For example all components can be deduced from 
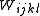the indices ijkl=2323, 2331, 1223, 1313, 1312 and 1212. The six components in such minimal sets are not independent as functions as they satisfy partial differential equations such as
and there are two further relations obtained by cyclic permutation.
In its simplest form of course the components of
must be assumed twice continuously differentiable, but more recent work proves the result in a much more general case.
The relation between Saint-Venant's compatibility condition and Poincare's lemma can be understood more clearly using the operator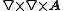
, where 
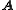is a symmetric tensor field. The matrix curl of a symmetric rank 2 tensor field T is defined by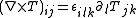
where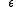
is the permutation symbol. The operator 
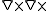maps symmetric tensor fields to symmetric tensor fields. The vanishing of the Saint Venant's tensor W(T) is equivalent to 
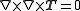. This illustrates more clearly the six independent components of W(T). The divergence of a tensor field 
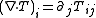satisfies 
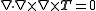. This exactly the three first order differential equations satisfied by the components of W(T) mentioned above.
In differential geometry the symmetrized derivative of a vector field appears also as the Lie derivative of the metric tensor g with respect to the vector field.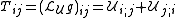
where indices following a semicolon indicate covariant differentiation. The vanishing of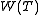
is thus the integrability condition for local existence of 
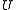in the Euclidean case.
s). The result can be generalized to higher rank symmetric tensor fields. Let F be a symmetric rank-k tensor field on an open set in n-dimensional Euclidean space
, then the symmetric derivative is the rank k+1 tensor field defined by
where we use the classical notation that indices following a comma indicate differentiation and groups of indices enclosed in brackets indicate symmetrization over those indices. The Saint-Venant tensor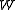
of a symmetric rank-k tensor field 
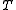is defined by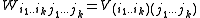
with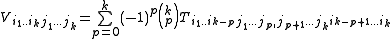
On a simply connected domain in Euclidean space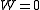
implies that 
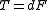for some rank k-1 symmetric tensor field 
.
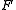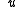is related to a displacement field by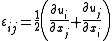Barré de Saint-Venant
Adhémar Jean Claude Barré de Saint-Venant
Adhémar Jean Claude Barré de Saint-Venant was a mechanician and mathematician who contributed to early stress analysis and also developed the one-dimensional unsteady open channel flow shallow water equations or Saint-Venant equations that are a fundamental set of equations used in modern...
derived the compatibility condition for an arbitrary symmetric second rank tensor field to be of this form, this has now been generalized to higher rank symmetric tensor fields.
Rank 2 tensor fields
The integrability condition takes the form of the vanishing of the Saint-Venant's tensor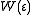 defined by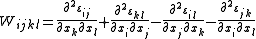The result that, on a simply connected domain W=0 implies that strain is the symmetric derivative of some vector field, was first described by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami
Beltrami
Beltrami may refer to:People*Eugenio Beltrami, Italian mathematician*Giacomo Beltrami, Italian count for whom the Minnesota county is named, and who claimed to have discovered the Mississippi River headwaters*Joseph Beltrami, Scottish lawyer...
in 1886. For non-simply connected domains there are finite dimensional spaces of symmetric tensors with vanishing Saint-Venant's tensor that are not the symmetric derivative of a vector field. The situation is analogous to de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
Due to the symmetry conditions
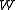there are only six (in the three dimensional case) distinct components of For example all components can be deduced from 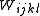the indices ijkl=2323, 2331, 1223, 1313, 1312 and 1212. The six components in such minimal sets are not independent as functions as they satisfy partial differential equations such asand there are two further relations obtained by cyclic permutation.
In its simplest form of course the components of
must be assumed twice continuously differentiable, but more recent work proves the result in a much more general case.The relation between Saint-Venant's compatibility condition and Poincare's lemma can be understood more clearly using the operator
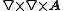, where 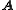is a symmetric tensor field. The matrix curl of a symmetric rank 2 tensor field T is defined by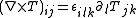where
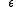is the permutation symbol. The operator 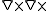maps symmetric tensor fields to symmetric tensor fields. The vanishing of the Saint Venant's tensor W(T) is equivalent to 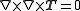. This illustrates more clearly the six independent components of W(T). The divergence of a tensor field 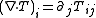satisfies 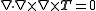. This exactly the three first order differential equations satisfied by the components of W(T) mentioned above.In differential geometry the symmetrized derivative of a vector field appears also as the Lie derivative of the metric tensor g with respect to the vector field.
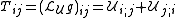
where indices following a semicolon indicate covariant differentiation. The vanishing of
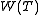is thus the integrability condition for local existence of 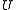in the Euclidean case.Generalization to higher rank tensors
Saint-Vanant's compatibility condition can be thought of as an analogue, for symmetric tensor fields, of Poincare's lemma for skew-symmetric tensor fields (differential formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s). The result can be generalized to higher rank symmetric tensor fields. Let F be a symmetric rank-k tensor field on an open set in n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, then the symmetric derivative is the rank k+1 tensor field defined by
where we use the classical notation that indices following a comma indicate differentiation and groups of indices enclosed in brackets indicate symmetrization over those indices. The Saint-Venant tensor
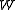of a symmetric rank-k tensor field 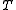is defined by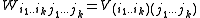with
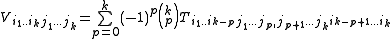
On a simply connected domain in Euclidean space
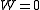implies that 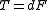for some rank k-1 symmetric tensor field .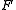