Rubik's Revenge - AbsoluteAstronomy.com

The Rubik's Revenge is the 4×4×4 version of Rubik's Cube

Rubik's Cube

Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...

. Invented by Péter Sebestény, the Rubik's Revenge was nearly called the Sebestény Cube until a somewhat last-minute decision changed the puzzle's name to attract fans of the original Rubik's Cube. Unlike the original puzzle (and the 5×5×5 cube

Professor's Cube

The Professor's Cube is a mechanical puzzle, a 5×5×5 version of the Rubik's Cube. It has qualities in common with both the original 3×3×3 Rubik's Cube and the 4×4×4 Rubik's Revenge, and knowing the solution to either can help when working on the 5×5×5 cube....

), it has no fixed facets: the centre facets (four per face) are free to move to different positions.

Methods for solving the 3×3×3 cube work for the edges and corners of the 4×4×4 cube, as long as one has correctly identified the relative positions of the colours — since the centre facets can no longer be used for identification.

Mechanics

The puzzle consists of the 56 unique miniature cubes ("cubies") on the surface. These consist of 24 centres which show one colour each, 24 edges which show two colours each, and 8 corners which show three colours each. The original Rubik's Revenge can be taken apart without much difficulty, typically by turning one side through a 30° angle and prying an edge upward until it dislodges.

The original mechanism designed by Sebestény uses a grooved ball to hold the centre pieces in place. The edge pieces are held in place by the centres and the corners are held in place by the edges, much like the original cube. There are three mutually perpendicular grooves for the centre pieces to slide through. Each groove is only wide enough to allow one row of centre pieces to slide through it. The ball is shaped to prevent the centre pieces of the other row from sliding, ensuring that the ball remains aligned with the outside of the cube. Turning one of the centre layers moves either just that layer or the ball as well.

The Eastsheen

Eastsheen

The Eastsheen cube is a mechanical puzzle that is meant to be smoother and faster than regular Rubik's cubes. They are preferred by most "Speedcubers"...

version of the cube, which is slightly smaller at 6 cm to an edge, has a completely different mechanism. Its mechanism is very similar to Eastsheen's version of the Professor's cube, instead of the ball-core mechanism. There are 42 pieces (36 movable and six fixed) completely hidden within the cube, corresponding to the centre rows on the Professor's Cube. This design is more durable than the original and also allows for screws to be used to tighten or loosen the cube. The central spindle is specially shaped to prevent it from becoming misaligned with the exterior of the cube.

There are 24 edge pieces which show two coloured sides each, and eight corner pieces which show three colours. Each corner piece or pair of edge pieces shows a unique colour combination, but not all combinations are present (for example, there is no piece with both red and orange sides, if red and orange are on opposite sides of the solved Cube). The location of these cubes relative to one another can be altered by twisting the layers of the cube, but the location of the coloured sides relative to one another in the completed state of the puzzle cannot be altered: it is fixed by the relative positions of the centre squares and the distribution of colour combinations on edge and corner pieces.

For most recent Cubes, the colours of the stickers are red opposite orange, yellow opposite white, and green opposite blue. However, there also exist Cubes with alternative colour arrangements (yellow opposite green, blue opposite white and red opposite orange). The Eastsheen version has purple (opposite red) instead of orange.

Permutations

There are 8 corners, 24 edges and 24 centres.

Any permutation of the corners is possible, including odd permutations. Seven of the corners can be independently rotated, and the orientation of the eighth depends on the other seven, giving 8!

Factorial

In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...

×3⁷ combinations.

There are 24 centres, which can be arranged in 24! different ways. Assuming that the four centres of each colour are indistinguishable, the number of permutations is reduced to 24!/(4!⁶) arrangements. The reducing factor comes about because there are 4! ways to arrange the four pieces of a given colour. This is raised to the sixth power because there are six colours. An odd permutation of the corners implies an odd permutation of the centres and vice versa; however, even and odd permutations of the centres are indistinguishable due to the identical appearance of the pieces. There are several ways to make the centre pieces distinguishable, which would make an odd centre permutation visible.

The 24 edges cannot be flipped, because the internal shape of the pieces is asymmetrical. Corresponding edges are distinguishable, since they are mirror images of each other. Any permutation of the edges is possible, including odd permutations, giving 24! arrangements, independently of the corners or centres.

Assuming the cube does not have a fixed orientation in space, and that the permutations resulting from rotating the cube without twisting it are considered identical, the number of permutations is reduced by a factor of 24. This is because all 24 possible positions and orientations of the first corner are equivalent because of the lack of fixed centres. This factor does not appear when calculating the permutations of N×N×N cubes where N is odd, since those puzzles have fixed centres which identify the cube's spatial orientation.

This gives a total number of permutations of

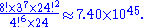
The full number is 7 401 196 841 564 901 869 874 093 974 498 574 336 000 000 000 possible permutations (about 7,401 septillion or 7.4 septilliard on the long scale

Names of large numbers

This article lists and discusses the usage and derivation of names of large numbers, together with their possible extensions.The following table lists those names of large numbers which are found in many English dictionaries and thus have a special claim to being "real words"...

or 7.4 quattuordecillion on the short scale).

Some versions of Rubik's Revenge have one of the centre pieces marked with a logo, distinguishing it from the other three of the same colour. This increases the number of distinguishable permutations by a factor of four to 2.96×10⁴⁶, although any of the four possible positions for this piece could be regarded as correct.

Solutions

There are several methods that can be used to solve a Rubik's Revenge. The layer by layer method that is often used for the 3×3×3 cube is usually used on the Rubik's Revenge. One of the most common methods is to first group the centre pieces of common colours together, then to pair edges that show the same two colours. Once this is done, turning only the outer layers of the cube allows it to be solved like a 3×3×3 cube. However, certain positions that cannot be solved on a standard 3×3×3 cube may be reached. There are two possible problems not found on the 3x3x3. The first is two edge pieces reversed on one edge, resulting in the colours for that edge not matching the rest of the cubies on either face:
Notice that these two edge pieces are swapped. The second is two edge pairs being swapped with each other:
These situations are known as parity errors. These positions are still solvable; however, special algorithms must be applied to fix the errors.

One of several approaches to solve this cube is to first pair the edges, and then the centres. This, too, is vulnerable to the parity errors described above.

Some methods are designed to avoid the parity errors described above. For instance, solving the corners and edges first and the centres last would avoid such parity errors. Once the rest of the cube is solved, any permutation of the centre pieces can be solved. Note that it is possible to apparently exchange a pair of face centres by cycling 3 face centres, two of which are visually identical.

World records

The world record for 4×4×4 Cube is held by Feliks Zemdegs

Feliks Zemdegs

Feliks Zemdegs is an Australian Rubik's Cube speedsolver. The surname is Latvian.He bought his first cube in April 2008 inspired by speedcubing videos and tutorials on Youtube. The first unofficial time he recorded was an average of 19.73 seconds on 14 June 2008...

of Australia with a time of 30.28 seconds set at the Australian Nationals 2011 in Melbourne, Australia. The best average time of 35.22 seconds is also held by Feliks Zemdegs

Feliks Zemdegs

of Australia set at the World Championships 2011. Daniel Sheppard of the UK holds the world record for solving the 4x4x4 cube blindfolded in 3 mins 26.11 seconds.

External links

Beginner/Intermediate solution to the Rubik's Revenge by Chris Hardwick
'K4' Method Advanced direct solving method.
Patterns A collection of pretty patterns for Rubik's Revenge
Program Rubik's Cube 3D Unlimited size

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Mechanics

Permutations

Solutions

World records

See also

Further reading

External links