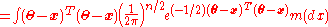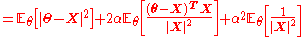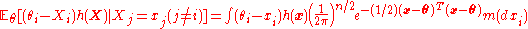Proof of Stein's example
Encyclopedia
Stein's example
is an important result in decision theory
which can be stated as
The following is an outline of its proof. The reader is referred to the main article
for more information.
of the decision rule is
is

Now consider the decision rule
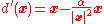
where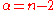 . We will show that
. We will show that 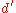 is a better decision rule than
is a better decision rule than 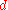 . The risk function is
. The risk function is
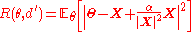
— a quadratic in . We may simplify the middle term by considering a general "well-behaved" function
. We may simplify the middle term by considering a general "well-behaved" function 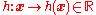 and using integration by parts
and using integration by parts
. For , for any continuously differentiable
, for any continuously differentiable 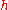 growing sufficiently slowly for large
growing sufficiently slowly for large 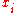 we have:
we have:
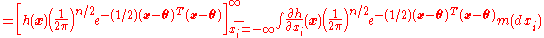
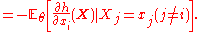
Therefore,
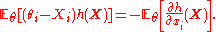
(This result is known as Stein's lemma
.)
Now, we choose
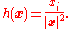
If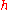 met the "well-behaved" condition (it doesn't, but this can be remedied -- see below), we would have
met the "well-behaved" condition (it doesn't, but this can be remedied -- see below), we would have
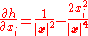
and so
Stein's example
Stein's example , in decision theory and estimation theory, is the phenomenon that when three or more parameters are estimated simultaneously, there exist combined estimators more accurate on average than any method that handles the parameters separately...
is an important result in decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
which can be stated as
- The ordinary decision rule for estimating the mean of a multivariate Gaussian distribution is inadmissible under mean squared error risk in dimension at least 3.
The following is an outline of its proof. The reader is referred to the main article
Stein's example
Stein's example , in decision theory and estimation theory, is the phenomenon that when three or more parameters are estimated simultaneously, there exist combined estimators more accurate on average than any method that handles the parameters separately...
for more information.
Sketched proof
The risk functionRisk function
In decision theory and estimation theory, the risk function R of a decision rule, δ, is the expected value of a loss function L:...
of the decision rule
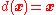 is
is
Now consider the decision rule
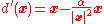
where
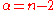 . We will show that
. We will show that 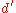 is a better decision rule than
is a better decision rule than 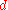 . The risk function is
. The risk function is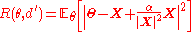
— a quadratic in
 . We may simplify the middle term by considering a general "well-behaved" function
. We may simplify the middle term by considering a general "well-behaved" function 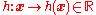 and using integration by parts
and using integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
. For
 , for any continuously differentiable
, for any continuously differentiable 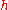 growing sufficiently slowly for large
growing sufficiently slowly for large 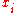 we have:
we have: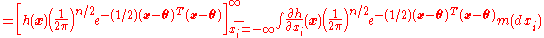
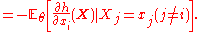
Therefore,
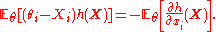
(This result is known as Stein's lemma
Stein's lemma
Stein's lemma, named in honor of Charles Stein, is a theorem of probability theory that is of interest primarily because of its applications to statistical inference — in particular, to James–Stein estimation and empirical Bayes methods — and its applications to portfolio choice...
.)
Now, we choose
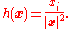
If
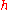 met the "well-behaved" condition (it doesn't, but this can be remedied -- see below), we would have
met the "well-behaved" condition (it doesn't, but this can be remedied -- see below), we would have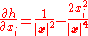
and so
-

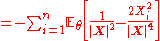
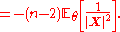
Then returning to the risk function of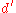 :
:
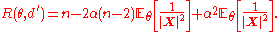
This quadratic in is minimized at
is minimized at
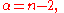
giving
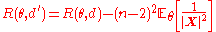
which of course satisfies:

making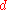 an inadmissible decision rule.
an inadmissible decision rule.
It remains to justify the use of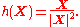
This function is not continuously differentiable since it is singular at . However the function
. However the function
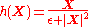
is continuously differentiable, and after following the algebra through and letting one obtains the same result.
one obtains the same result.