Professor's Cube
Encyclopedia
The Professor's Cube is a mechanical puzzle
, a 5×5×5 version of the Rubik's Cube
. It has qualities in common with both the original 3×3×3 Rubik's Cube
and the 4×4×4 Rubik's Revenge
, and knowing the solution to either can help when working on the 5×5×5 cube.
The original Professor's Cube design by Udo Krell works by using an expanded 3×3×3 cube as a mantle with the center edge pieces and corners sticking out from the spherical center of identical mechanism to the 3×3×3 cube. All non-central pieces have extensions that fit into slots on the outer pieces of the 3×3×3, which keeps them from falling out of the cube while making a turn. The fixed centers have two sections (one visible, one hidden) which can turn independently. This feature is unique to the original design.
The Eastsheen
version of the puzzle uses a different mechanism. The fixed centers hold the centers next to the central edges in place, which in turn hold the outer edges. The non-central edges hold the corners in place, and the internal sections of the corner pieces do not reach the center of the cube.
The V-Cube 5 mechanism, designed by Panagiotis Verdes, has elements in common with both. The corners reach to the center of the puzzle (like the original mechanism) and the center pieces hold the central edges in place (like the Eastsheen mechanism). The middle edges and center pieces adjacent to them make up the supporting frame and these have extensions which hold rest of the pieces together. This allows smooth and fast rotation and creating arguably the fastest and most durable version of the puzzle. Unlike the original 5×5×5 design, the V-Cube 5 mechanism was designed with speedcubing
in mind.
. The puzzle should not be excessively forced to twist and it must be aligned properly before twisting to prevent damage. It is far more likely to break due to twisting misaligned rows. If twisted while not fully aligned, it may cause the pieces diagonal to the corners to almost fully come out. It is simply fixed by turning the face back to where it was, causing the piece to go back to its original position. Excessive force may cause the colored tile to break off completely. In such a case, the puzzle will not fall apart, but a colored square would be gone. Both the Eastsheen 5×5×5 and the V-Cube 5 are designed with different mechanisms in an attempt to remedy the fragility of the original design.
Any permutation
of the corners is possible, including odd permutations, giving 8!
possible arrangements. Seven of the corners can be independently rotated, and the orientation of the eighth depends on the other seven, giving 37 combinations.
There are 54 centers. Six of these (the center square of each face) are fixed in position. The rest consist of two sets of 24 centers. Within each set there are four centers of each color. Each set can be arranged in 24! different ways. Assuming that the four centers of each color in each set are indistinguishable, the number of permutations of each set is reduced to 24!/(4!6) arrangements, all of which are possible. The reducing factor comes about because there are 4! ways to arrange the four pieces of a given color. This is raised to the sixth power because there are six colors. The total number of permutations of all movable centers is the product of the permutations of the two sets, 24!2/(4!12).
The 24 outer edges cannot be flipped, since the interior shape of those pieces is asymmetrical. Corresponding outer edges are distinguishable, since the pieces are mirror images of each other. Any permutation of the outer edges is possible, including odd permutations, giving 24! arrangements. The 12 central edges can be flipped. Eleven can be flipped and arranged independently, giving 12!/2 × 211 or 12! × 210 possibilities (an odd permutation of the corners implies an odd permutation of the central edges, and vice versa, thus the division by 2). There are 24! × 12! × 210 possibilities for the inner and outer edges together.
This gives a total number of permutations of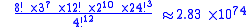
The full number is precisely 282 870 942 277 741 856 536 180 333 107 150 328 293 127 731 985 672 134 721 536 000 000 000 000 000 possible permutations (about 283 duodecillion on the long scale
or 283 tresvigintillion on the short scale).
Some variations of the Professor's Cube have one of the center pieces marked with a logo, which can be put into four different orientations. This increases the number of permutations by a factor of four to 1.13×1075, although any orientation of this piece could be regarded as correct. Other variations increase the difficulty by making the orientation of all center pieces visible. An example of this is shown below.
People able to rapidly solve puzzles like this usually favour the strategy of grouping similar edge pieces into solid strips, and centers into one-colored blocks. This allows the cube to be quickly solved with the same methods one would use for a 3×3×3 cube. As illustrated to the right, the fixed centers, middle edges and corners can be treated as equivalent to a 3×3×3 cube. As a result, the parity errors sometimes seen on the 4×4×4 cannot occur on the 5×5×5 unless the cube has been tampered with.
Another frequently used strategy is to solve the edges of the cube first. The corners can be placed just as they are in any previous order of cube puzzle, and the centers are manipulated with an algorithm similar to the one used in the 4×4×4 cube.
A less frequently used strategy is to solve one side and one rim first, then the 2nd, 3rd and 4th rim, and finally the last side and rim. That is, like building a four floor building. First the basement, then each floor, and finally the roof. This method is among other described at.
from Australia, at the World Championship 2011. He also holds the current world record for an average of five solves, 59.94 seconds, set at the same event.
Puzzle
A puzzle is a problem or enigma that tests the ingenuity of the solver. In a basic puzzle, one is intended to put together pieces in a logical way in order to come up with the desired solution...
, a 5×5×5 version of the Rubik's Cube
Rubik's Cube
Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
. It has qualities in common with both the original 3×3×3 Rubik's Cube
Rubik's Cube
Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
and the 4×4×4 Rubik's Revenge
Rubik's Revenge
The Rubik's Revenge is the 4×4×4 version of Rubik's Cube. Invented by Péter Sebestény, the Rubik's Revenge was nearly called the Sebestény Cube until a somewhat last-minute decision changed the puzzle's name to attract fans of the original Rubik's Cube...
, and knowing the solution to either can help when working on the 5×5×5 cube.
Naming
Early versions of the 5×5×5 cube sold at Barnes and Noble were marketed under the name "Professor's Cube," but currently, Barnes and Noble sells cubes that are simply called "5×5." Mefferts.com offers a limited edition version of the 5×5×5 cube called the Professor's Cube. This version has colored tiles rather than stickers. Verdes Innovations sells a version called the V-Cube 5.Workings
The Eastsheen
Eastsheen
The Eastsheen cube is a mechanical puzzle that is meant to be smoother and faster than regular Rubik's cubes. They are preferred by most "Speedcubers"...
version of the puzzle uses a different mechanism. The fixed centers hold the centers next to the central edges in place, which in turn hold the outer edges. The non-central edges hold the corners in place, and the internal sections of the corner pieces do not reach the center of the cube.
The V-Cube 5 mechanism, designed by Panagiotis Verdes, has elements in common with both. The corners reach to the center of the puzzle (like the original mechanism) and the center pieces hold the central edges in place (like the Eastsheen mechanism). The middle edges and center pieces adjacent to them make up the supporting frame and these have extensions which hold rest of the pieces together. This allows smooth and fast rotation and creating arguably the fastest and most durable version of the puzzle. Unlike the original 5×5×5 design, the V-Cube 5 mechanism was designed with speedcubing
Speedcubing
Speedcubing is the activity of solving a Rubik's Cube or related puzzle as quickly as possible...
in mind.
Durability
The original Professor's Cube is inherently more delicate than the 3×3×3 Rubik's Cube due to the much greater number of moving parts. It is not recommended that it be used for speedcubingSpeedcubing
Speedcubing is the activity of solving a Rubik's Cube or related puzzle as quickly as possible...
. The puzzle should not be excessively forced to twist and it must be aligned properly before twisting to prevent damage. It is far more likely to break due to twisting misaligned rows. If twisted while not fully aligned, it may cause the pieces diagonal to the corners to almost fully come out. It is simply fixed by turning the face back to where it was, causing the piece to go back to its original position. Excessive force may cause the colored tile to break off completely. In such a case, the puzzle will not fall apart, but a colored square would be gone. Both the Eastsheen 5×5×5 and the V-Cube 5 are designed with different mechanisms in an attempt to remedy the fragility of the original design.
Permutations
There are 98 pieces on the exterior of the cube: 8 corners, 36 edges, and 54 centers (48 movable, 6 fixed).Any permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the corners is possible, including odd permutations, giving 8!
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
possible arrangements. Seven of the corners can be independently rotated, and the orientation of the eighth depends on the other seven, giving 37 combinations.
There are 54 centers. Six of these (the center square of each face) are fixed in position. The rest consist of two sets of 24 centers. Within each set there are four centers of each color. Each set can be arranged in 24! different ways. Assuming that the four centers of each color in each set are indistinguishable, the number of permutations of each set is reduced to 24!/(4!6) arrangements, all of which are possible. The reducing factor comes about because there are 4! ways to arrange the four pieces of a given color. This is raised to the sixth power because there are six colors. The total number of permutations of all movable centers is the product of the permutations of the two sets, 24!2/(4!12).
The 24 outer edges cannot be flipped, since the interior shape of those pieces is asymmetrical. Corresponding outer edges are distinguishable, since the pieces are mirror images of each other. Any permutation of the outer edges is possible, including odd permutations, giving 24! arrangements. The 12 central edges can be flipped. Eleven can be flipped and arranged independently, giving 12!/2 × 211 or 12! × 210 possibilities (an odd permutation of the corners implies an odd permutation of the central edges, and vice versa, thus the division by 2). There are 24! × 12! × 210 possibilities for the inner and outer edges together.
This gives a total number of permutations of
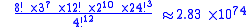
The full number is precisely 282 870 942 277 741 856 536 180 333 107 150 328 293 127 731 985 672 134 721 536 000 000 000 000 000 possible permutations (about 283 duodecillion on the long scale
Names of large numbers
This article lists and discusses the usage and derivation of names of large numbers, together with their possible extensions.The following table lists those names of large numbers which are found in many English dictionaries and thus have a special claim to being "real words"...
or 283 tresvigintillion on the short scale).
Some variations of the Professor's Cube have one of the center pieces marked with a logo, which can be put into four different orientations. This increases the number of permutations by a factor of four to 1.13×1075, although any orientation of this piece could be regarded as correct. Other variations increase the difficulty by making the orientation of all center pieces visible. An example of this is shown below.
Solution
Another frequently used strategy is to solve the edges of the cube first. The corners can be placed just as they are in any previous order of cube puzzle, and the centers are manipulated with an algorithm similar to the one used in the 4×4×4 cube.
A less frequently used strategy is to solve one side and one rim first, then the 2nd, 3rd and 4th rim, and finally the last side and rim. That is, like building a four floor building. First the basement, then each floor, and finally the roof. This method is among other described at.
World records
The current record for solving the Professor's Cube in an official competition is 56.22 seconds, set by Feliks ZemdegsFeliks Zemdegs
Feliks Zemdegs is an Australian Rubik's Cube speedsolver. The surname is Latvian.He bought his first cube in April 2008 inspired by speedcubing videos and tutorials on Youtube. The first unofficial time he recorded was an average of 19.73 seconds on 14 June 2008...
from Australia, at the World Championship 2011. He also holds the current world record for an average of five solves, 59.94 seconds, set at the same event.
See also
- Pocket CubePocket CubeThe Pocket Cube is the 2×2×2 equivalent of a Rubik's Cube. The cube consists of 8 pieces, all corners.-Permutations:...
– A 2×2×2 version of the puzzle - Rubik's CubeRubik's CubeRubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
– The 3×3×3 original version of this puzzle - Rubik's RevengeRubik's RevengeThe Rubik's Revenge is the 4×4×4 version of Rubik's Cube. Invented by Péter Sebestény, the Rubik's Revenge was nearly called the Sebestény Cube until a somewhat last-minute decision changed the puzzle's name to attract fans of the original Rubik's Cube...
– A 4×4×4 version of the puzzle - V-Cube 6V-Cube 6The V-Cube 6 is the 6×6×6 version of Rubik's Cube. Unlike the original puzzle , it has no fixed facets: the center facets are free to move to different positions...
- A 6×6×6 version of the puzzle - V-Cube 7V-Cube 7The V-Cube 7 is the 7×7×7 version of Rubik's Cube. It was invented by Panagiotis Verdes and is produced by his company, Verdes Innovations SA. Like the 5×5×5, the V-Cube 7 has both fixed and movable center facets.- Mechanics :...
- A 7×7×7 version of the puzzle - Combination puzzlesCombination puzzlesA combination puzzle, also known as a sequential move puzzle, is a puzzle which consists of a set of pieces which can be manipulated into different combinations by a group of operations. The puzzle is solved by achieving a particular combination starting from a random combination...