
Poncelet's porism
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
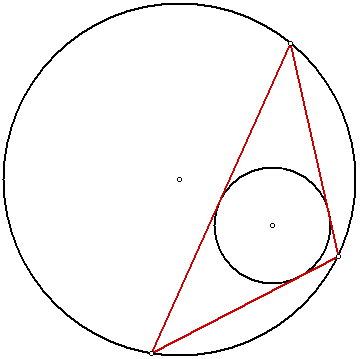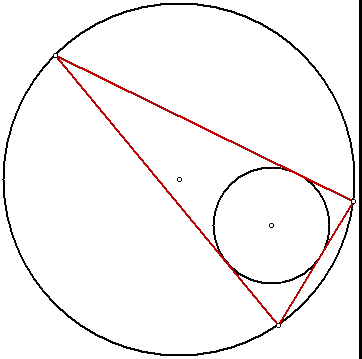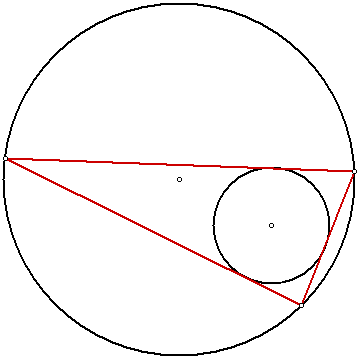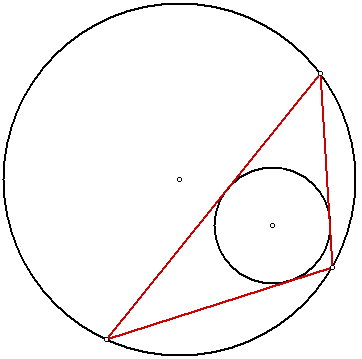
, Poncelet's porism, named after French engineer and mathematician Jean-Victor Poncelet
Jean-Victor Poncelet
Jean-Victor Poncelet was a French engineer and mathematician who served most notably as the commandant general of the École Polytechnique...
, states the following: Let C and D be two plane conics. If it is possible to find, for a given n > 2, one n-sided polygon that is simultaneously inscribed in C and circumscribed around D, then it is possible to find infinitely many of them.
Poncelet's porism
Porism
A porism is a mathematical proposition or corollary. In particular, the term porism has been used to refer to a direct result of a proof, analogous to how a corollary refers to a direct result of a theorem.-Beginnings:...
can be proved via elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s; geometrically this depends on the representation of an elliptic curve as the double cover of C with four ramification points. (Note that C is isomorphic to the complex projective line.) The relevant ramification is over the four points of C where the conics intersect. (There are four such points by Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
.) One can also describe the elliptic curve as a double cover of D; in this case, the ramification is over the contact points of the four bitangents.
Proof
Let p be a point of P2 and ℓ a line of the dual projective plane. The key tool is the curve X given by the set of pairs (p, ℓ) where p is on the conic C and ℓ is tangent to the conic D. Then X is smooth; more specifically X is an elliptic curve. There is an involution of X mapping (p, ℓ) to (p
of X mapping (p, ℓ) to (p that sends (p, ℓ) to (p, ℓ
that sends (p, ℓ) to (p, ℓ is a translation. If it has one fixed point, it must be the identity. Translated back into the language of C and D, this means that if one point on C gives rise to an orbit that closes up (i.e. gives an n-gon), then every point does, as well.
is a translation. If it has one fixed point, it must be the identity. Translated back into the language of C and D, this means that if one point on C gives rise to an orbit that closes up (i.e. gives an n-gon), then every point does, as well.External links
- David Speyer on Poncelet's Porism
- D. Fuchs, S. Tabachnikov, Mathematical Omnibus: Thirty Lectures on Classic Mathematics
- Java applet by Michael Borcherds showing the cases n = 3, 4, 5, 6, 7, 8 (including the convex cases for n = 7, 8) made using GeoGebra.
- Java applet by Michael Borcherds showing Poncelet's Porism for a general Ellipse and a Parabola made using GeoGebra.
- Java applet by Michael Borcherds showing Poncelet's Porism for 2 general ellipses (order 3) made using GeoGebra.
- Java applet by Michael Borcherds showing Poncelet's Porism for 2 general ellipses (order 5) made using GeoGebra.
- Java applet by Michael Borcherds showing Poncelet's Porism for 2 general ellipses (order 6) made using GeoGebra.
- Java applet showing the exterior case for n = 3 at National Tsing Hua University.
- Article on Poncelet's Porism at Mathworld.

