Numerov's method
Encyclopedia
Numerov's method is a numerical method to solve ordinary differential equation
s of second order in which the first-order term does not appear. It is a fourth-order linear multistep method. The method is implicit, but can be made explicit if the differential equation is linear.
Numerov's method was developed by Boris Vasil'evich Numerov
.
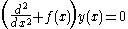
The function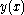
is sampled in the interval [a..b] at equidistant positions 
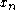. Starting from function values at two consecutive samples 
and 
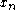the remaining function values can be calculated as
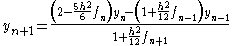
where
and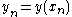 
are the function values at the positions 
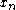and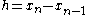 
is the distance between two consecutive samples.
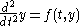
the method is given by
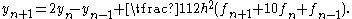
This is an implicit linear multistep method, which reduces to the explicit method given above if the function f is linear in y. It achieves order 4 .
for arbitrary potentials.
The above equation can be rewritten in the form
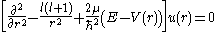
with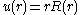
. If we compare this equation with the defining equation of the Numerov method we see
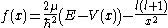
and thus can numerically solve the radial Schrödinger equation.
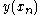we get for the two sampling points adjacent to 
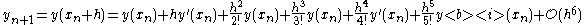
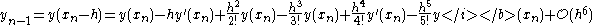
The sum of those two equations gives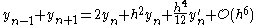
We solve this equation for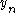
and replace it by the expression 
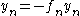which we get from the defining differential equation.
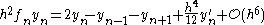
We take the second derivative of our defining differential equation and get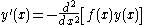
We replace the second derivative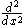
with the second order difference quotient
and insert this into our equation for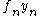
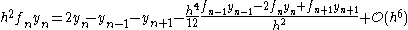
We solve for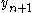
to get
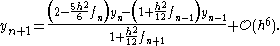
This yields Numerov's method if we ignore the term of order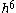
. It follows that the order of convergence (assuming stability) is 4.
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s of second order in which the first-order term does not appear. It is a fourth-order linear multistep method. The method is implicit, but can be made explicit if the differential equation is linear.
Numerov's method was developed by Boris Vasil'evich Numerov
Boris Vasil'evich Numerov
Boris Vasilyevich Numerov was a Russian astronomer, land-surveyor and geophysicist. Born in Lyuban, he created various astronomic and mineralogical instruments, as well as for various algorithms and methods that bear his name...
.
The method
The Numerov method can be used to solve differential equations of the form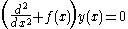The function
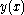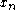is sampled in the interval [a..b] at equidistant positions . Starting from function values at two consecutive samples and the remaining function values can be calculated as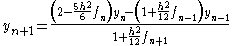where
and 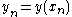are the function values at the positions 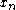and 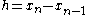is the distance between two consecutive samples.Nonlinear equations
For nonlinear equations of the form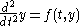the method is given by
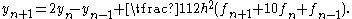
This is an implicit linear multistep method, which reduces to the explicit method given above if the function f is linear in y. It achieves order 4 .
Application
In numerical physics the method is used to find solutions of the radial Schrödinger EquationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for arbitrary potentials.
The above equation can be rewritten in the form
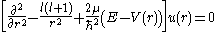
with
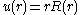. If we compare this equation with the defining equation of the Numerov method we see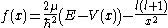and thus can numerically solve the radial Schrödinger equation.
Derivation
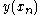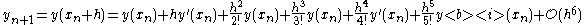
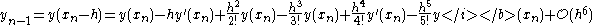
Starting from the Taylor expansion for we get for the two sampling points adjacent to The sum of those two equations gives
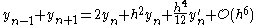
We solve this equation for
and replace it by the expression which we get from the defining differential equation.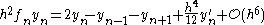We take the second derivative of our defining differential equation and get
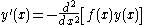
We replace the second derivative
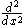with the second order difference quotientDifference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
and insert this into our equation for
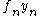
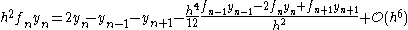
We solve for
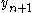to get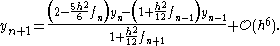This yields Numerov's method if we ignore the term of order
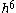. It follows that the order of convergence (assuming stability) is 4.External links
- Lecture notes: Computerphysik und Numerik - by Jan Krieger
- Lecture notes of Werner Scholz - At Vienna University of Technology
- Lecture notes of Alexander Wagner