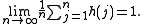Niven's constant
Encyclopedia
In number theory
, Niven's constant, named after Ivan Niven, is the largest exponent appearing in the prime factorization of any natural number n "on average". More precisely, if we define H(1) = 1 and H(n) = the largest exponent appearing in the unique prime factorization of a natural number n > 1, then Niven's constant is given by
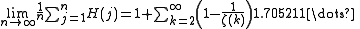
where ζ(k) is the value of the Riemann zeta function at the point k (Niven, 1969).
In the same paper Niven
also proved that
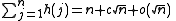
where h(1) = 1, h(n) = the smallest exponent appearing in the unique prime factorization of each natural number n > 1, o is little o notation, and the constant c is given by

and consequently that
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Niven's constant, named after Ivan Niven, is the largest exponent appearing in the prime factorization of any natural number n "on average". More precisely, if we define H(1) = 1 and H(n) = the largest exponent appearing in the unique prime factorization of a natural number n > 1, then Niven's constant is given by
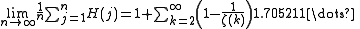
where ζ(k) is the value of the Riemann zeta function at the point k (Niven, 1969).
In the same paper Niven
Ivan M. Niven
Ivan Morton Niven was a Canadian-American mathematician, specializing in number theory. He was born in Vancouver. He did his undergraduate studies at the University of British Columbia and was awarded his doctorate in 1938 from the University of Chicago. He was a member of the University of Oregon...
also proved that
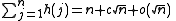
where h(1) = 1, h(n) = the smallest exponent appearing in the unique prime factorization of each natural number n > 1, o is little o notation, and the constant c is given by

and consequently that