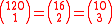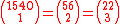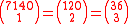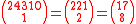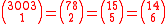Multiplicities of entries in Pascal's triangle
Encyclopedia
In combinatorial number theory, Singmaster's conjecture, named after David Singmaster
, says there is a finite upper bound on the multiplicities
of entries in Pascal's triangle
(other than the number 1, which appears infinitely many times). It is clear that the only number that appears infinitely many times in Pascal's triangle
is 1, because any other number x can appear only within the first x + 1 rows of the triangle. Paul Erdős
said that Singmaster's conjecture is probably true but he suspected it would be very hard to prove.
Let N(a) be the number of times the number a > 1 appears in Pascal's triangle. In big O notation
, the conjecture is:


Abbot, Erdős
, and Hanson (see References) refined the estimate. The best currently known (unconditional) bound is
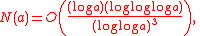
and is due to Kane (2007). Abbot, Erdős, and Hanson note that conditional on Cramér's conjecture on gaps between consecutive primes that
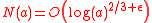
holds for any .
.
Singmaster (1975) showed that the Diophantine equation
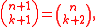
has infinitely many solutions for the two variables n, k. It follows that there are infinitely many entries of multiplicity at least 6. The solutions are given by

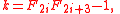
where Fn is the nth Fibonacci number
(indexed according to the convention that F1 = F2 = 1).
The next number in Singmaster's infinite family, and the next smallest number known to occur six or more times, is 61218182743304701891431482520.
It is not known whether any number appears more than eight times, nor whether any number besides 3003 appears that many times. The conjectured finite upper bound could be as small as 8, but Singmaster thought it might be 10 or 12.
David Singmaster
David Breyer Singmaster is a retired professor of mathematics at London South Bank University, England, UK. A self-described metagrobologist, he is most famous for his solution to the Rubik's cube and his huge personal collection of mechanical puzzles and books of brain teasers. He is also...
, says there is a finite upper bound on the multiplicities
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of entries in Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
(other than the number 1, which appears infinitely many times). It is clear that the only number that appears infinitely many times in Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
is 1, because any other number x can appear only within the first x + 1 rows of the triangle. Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
said that Singmaster's conjecture is probably true but he suspected it would be very hard to prove.
Let N(a) be the number of times the number a > 1 appears in Pascal's triangle. In big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, the conjecture is:

Known results
Singmaster (1971) showed that
Abbot, Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
, and Hanson (see References) refined the estimate. The best currently known (unconditional) bound is
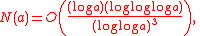
and is due to Kane (2007). Abbot, Erdős, and Hanson note that conditional on Cramér's conjecture on gaps between consecutive primes that
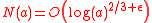
holds for any
 .
.Singmaster (1975) showed that the Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
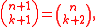
has infinitely many solutions for the two variables n, k. It follows that there are infinitely many entries of multiplicity at least 6. The solutions are given by

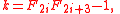
where Fn is the nth Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
(indexed according to the convention that F1 = F2 = 1).
Numerical examples
Computation tells us that- 2 appears just once; all larger positive integers appear more than once;
- 3, 4, 5 each appear 2 times;
- 6 appears 3 times;
- Many numbers appear 4 times.
- Each of the following appears 6 times:
- The smallest number to appear 8 times is 3003, which is also the first member of Singmaster's infinite family of numbers with multiplicity at least 6:
The next number in Singmaster's infinite family, and the next smallest number known to occur six or more times, is 61218182743304701891431482520.
It is not known whether any number appears more than eight times, nor whether any number besides 3003 appears that many times. The conjectured finite upper bound could be as small as 8, but Singmaster thought it might be 10 or 12.