Lotka's law
Encyclopedia
Lotka's law, named after Alfred J. Lotka
, is one of a variety of special applications of Zipf's law. It describes the frequency of publication by authors in any given field. It states that the number of authors making n contributions is about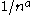
of those making one contribution, where a nearly always equals two. More plainly, the number of authors publishing a certain number of articles is a fixed ratio to the number of authors publishing a single article. As the number of articles published increases, authors producing that many publications become less frequent. There are 1/4 as many authors publishing two articles within a specified time period as there are single-publication authors, 1/9 as many publishing three articles, 1/16 as many publishing four articles, etc. Though the law itself covers many disciplines, the actual ratios involved (as a function of 'a') are very discipline-specific.
The general formula says:
or
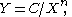
where X is the number of publications, Y the relative frequency of authors with X publications, and n and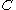
are constants depending on the specific field (
).
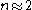This law is believed to have applications in other fields, for example in the military for fighter pilot kills.
That would be a total of 293 articles with 155 writers with an average of 1.9 articles for each writer.
This is an empirical observation rather than a necessary result. This form of the law is as originally published and is sometimes referred to as the "discrete Lotka power function".
", and equating it to the maxim that "success breeds success".
Alfred J. Lotka
Alfred James Lotka was a US mathematician, physical chemist, and statistician, famous for his work in population dynamics and energetics. An American biophysicist best known for his proposal of the predator-prey model, developed simultaneously but independently of Vito Volterra...
, is one of a variety of special applications of Zipf's law. It describes the frequency of publication by authors in any given field. It states that the number of authors making n contributions is about
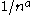of those making one contribution, where a nearly always equals two. More plainly, the number of authors publishing a certain number of articles is a fixed ratio to the number of authors publishing a single article. As the number of articles published increases, authors producing that many publications become less frequent. There are 1/4 as many authors publishing two articles within a specified time period as there are single-publication authors, 1/9 as many publishing three articles, 1/16 as many publishing four articles, etc. Though the law itself covers many disciplines, the actual ratios involved (as a function of 'a') are very discipline-specific.The general formula says:
or
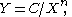
where X is the number of publications, Y the relative frequency of authors with X publications, and n and
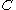are constants depending on the specific field (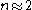).This law is believed to have applications in other fields, for example in the military for fighter pilot kills.
Example
Say 100 authors write one article each over a specific period, we assume for this table that C=1 and n=2:| Number of articles written | Number of authors writing that number of articles |
|---|---|
| 10 | 100/102 = 1 |
| 9 | 100/92 ≈ 1 (1.23) |
| 8 | 100/82 ≈ 2 (1.56) |
| 7 | 100/72 ≈ 2 (2.04) |
| 6 | 100/62 ≈ 3 (2.77) |
| 5 | 100/52 = 4 |
| 4 | 100/42 ≈ 6 (6.25) |
| 3 | 100/32 ≈ 11 (11.111...) |
| 2 | 100/22 = 25 |
| 1 | 100 |
That would be a total of 293 articles with 155 writers with an average of 1.9 articles for each writer.
This is an empirical observation rather than a necessary result. This form of the law is as originally published and is sometimes referred to as the "discrete Lotka power function".
Further reading
— Chung and Cox analyze a bibliometric regularity in finance literature, relating Lotka's law to the maxim that "the rich get richer and the poor get poorerThe rich get richer and the poor get poorer
"The rich get richer and the poor get poorer" is a catchphrase and proverb, frequently used in discussing economic inequality...
", and equating it to the maxim that "success breeds success".