List of Hund's rules
Encyclopedia
In atomic physics
, Hund's rules refer to a set of rules formulated by German physicist Friedrich Hund
around 1927, which are used to determine the term symbol
that corresponds to the ground state of a multi-electron
atom
. In chemistry, rule one is especially important and is often referred to as simply Hund's Rule
.
The three rules are:
These rules specify in a simple way how the usual energy interactions dictate the ground state term. The rules assume that the repulsion between the outer electrons is very much greater than the spin-orbit interaction which is in turn stronger than any other remaining interactions. This is referred to as the LS coupling regime.
Full shells and subshells do not contribute to the quantum numbers for total S, the total spin angular momentum and for L, the total orbital angular momentum. It can be shown that for full orbitals and suborbitals both the residual electrostatic term (repulsion between electrons) and the spin-orbit interaction can only shift all the energy levels together. Thus when determining the ordering of energy levels in general only the outer valence electrons need to be considered.
, two electrons cannot share the same set of quantum numbers within the same system. Therefore, there is room for only two electrons in each spatial orbital. One of these electrons must have (for some chosen direction z),
, and the other must have 
. Hund's first rule states that the lowest energy atomic state is the one which maximizes the sum of the 
values for all of the electrons in the open subshell. The orbitals of the subshell are each occupied singly with electrons of parallel spin before double occupation occurs. (This is occasionally called the "bus seat rule" since it is analogous to the behaviour of bus passengers who tend to occupy all double seats singly before double occupation occurs.)
Two physical explanations have been given for the increased stability of high multiplicity states. In the early days of quantum mechanics
, it was proposed that electrons in different orbitals are further apart, so that electron-electron repulsion energy is reduced. However this explanation is now obsolete. Accurate quantum-mechanical calculations (starting in the 1970s) have shown that the true reason is that the electrons in singly occupied orbitals are less effectively screened or shielded
from the nucleus, so that such orbitals contract and electron-nuclear attraction energy becomes greater in magnitude (or decreases algebraically).
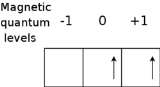
As an example, consider the ground state of silicon
. The electronic configuration of Si is
. We need consider only the outer 
electrons, for which it can be shown (see term symbols) that the possible terms allowed by the Pauli exclusion principle
are
. Hund's first rule now states that the ground state term is 
which has 
. The superscript 3 is the value of the multiplicity = 2S + 1 = 3. The diagram shows the state of this term with ML = 1 and MS = 1.
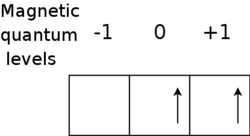
s
, so the second rule is not required. The lightest atom which requires the second rule to determine the ground state is titanium
(Ti, Z = 22) with electron configuration 1s2 2s2 2p6 3s2 3p6 4s2 3d2. Following the same method as for Si, the allowed terms include three singlets (1S, 1D, and 1G)
and two triplets (3P and 3F). We deduce from Hund's first rule that the ground state is one of the two triplets, and from Hund's second rule that the ground state is 3F (with L = 3) rather than 3P (with L = 1). There is no
3G term since its (ML = 4, MS = 1) state would require two electrons each with (ML = 2, MS = +1/2), in violation of the Pauli principle.
and 
are still good quantum numbers and the splitting is given by:
The value of
changes from plus to minus for shells greater than half full. This term gives the dependence of the ground state energy on the magnitude of 
.
lowest energy term of Si consists of three levels, 
. With only two of six possible electrons in the shell, it is less than half-full and thus 
is the ground state.
For sulfur
(S) the lowest energy term is again
with spin-orbit levels 
, but now there are four of six possible electrons in the shell so the ground state is 
.
If the shell is half-filled then
, and hence there is only one value of 
(equal to 
) which will be the lowest energy state. For example in phosphorus
the lowest energy state has
for three unpaired electrons in three 2p orbitals. Therefore 
and the ground state is 4S3/2.
of an atom or molecule.
They are also fairly reliable (with occasional failures) for the determination of the lowest state of a given excited electronic configuration. Thus in the helium atom, the 1s2s triplet state (3S) is correctly predicted by Hund's first rule to be lower than the 1s2s singlet (1S). Similarly for organic molecules, the same rule predicts that the first triplet state (denoted by T1 in photochemistry
) is lower than the first excited singlet state (S1), which is generally correct.
However Hund's rules should not be used to order states other than the lowest for a given configuration. For example, the titanium
atom ground state configuration is ...3d2 for which a naïve application of Hund's rules would suggest the ordering 3F < 3P < 1G < 1D < 1S. In reality, however, 1D lies below 1G.
For the notation of orbital angular momentum L see: Spectroscopic notation
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
, Hund's rules refer to a set of rules formulated by German physicist Friedrich Hund
Friedrich Hund
Friedrich Hermann Hund was a German physicist from Karlsruhe known for his work on atoms and molecules.Hund worked at the Universities of Rostock, Leipzig, Jena, Frankfurt am Main, and Göttingen....
around 1927, which are used to determine the term symbol
Term symbol
In quantum mechanics, the Russell-Saunders term symbol is an abbreviated description of the angular momentum quantum numbers in a multi-electron atom. It is related with the energy level of a given electron configuration. LS coupling is assumed...
that corresponds to the ground state of a multi-electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
. In chemistry, rule one is especially important and is often referred to as simply Hund's Rule
Hund's rule of Maximum Multiplicity
Hund's Rule of Maximum Multiplicity is an observational rule which states that a greater total spin state usually makes the resulting atom more stable. Accordingly, it can be taken that if two or more orbitals of equal energy are available, electrons will occupy them singly before filling them in...
.
The three rules are:
- For a given electron configuration, the term with maximum multiplicityMultiplicity (chemistry)Multiplicity in quantum chemistry is used to distinguish between several degenerate wavefunctions that differ only in the orientation of their angular spin momenta. It is defined as 2S+1, where S is the angular spin momentum....
has the lowest energy. Since multiplicity is equal to
, this is also the term with maximum 
. 
is the spin angular momentum. - For a given multiplicity, the term with the largest value of
has the lowest energy, where 
is the orbital angular momentum. - For a given term, in an atom with outermost subshell half-filled or less, the level with the lowest value of
lies lowest in energy. If the outermost shell is more than half-filled, the level with highest value of 
is lowest in energy. 
is the total angular momentum, 
.
These rules specify in a simple way how the usual energy interactions dictate the ground state term. The rules assume that the repulsion between the outer electrons is very much greater than the spin-orbit interaction which is in turn stronger than any other remaining interactions. This is referred to as the LS coupling regime.
Full shells and subshells do not contribute to the quantum numbers for total S, the total spin angular momentum and for L, the total orbital angular momentum. It can be shown that for full orbitals and suborbitals both the residual electrostatic term (repulsion between electrons) and the spin-orbit interaction can only shift all the energy levels together. Thus when determining the ordering of energy levels in general only the outer valence electrons need to be considered.
Rule #1
Due to the Pauli exclusion principlePauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, two electrons cannot share the same set of quantum numbers within the same system. Therefore, there is room for only two electrons in each spatial orbital. One of these electrons must have (for some chosen direction z),
, and the other must have . Hund's first rule states that the lowest energy atomic state is the one which maximizes the sum of the values for all of the electrons in the open subshell. The orbitals of the subshell are each occupied singly with electrons of parallel spin before double occupation occurs. (This is occasionally called the "bus seat rule" since it is analogous to the behaviour of bus passengers who tend to occupy all double seats singly before double occupation occurs.)Two physical explanations have been given for the increased stability of high multiplicity states. In the early days of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, it was proposed that electrons in different orbitals are further apart, so that electron-electron repulsion energy is reduced. However this explanation is now obsolete. Accurate quantum-mechanical calculations (starting in the 1970s) have shown that the true reason is that the electrons in singly occupied orbitals are less effectively screened or shielded
Effective nuclear charge
The effective nuclear charge is the net positive charge experienced by an electron in a multi-electron atom. The term "effective" is used because the shielding effect of negatively charged electrons prevents higher orbital electrons from experiencing the full nuclear charge by the repelling effect...
from the nucleus, so that such orbitals contract and electron-nuclear attraction energy becomes greater in magnitude (or decreases algebraically).
Example
Silicon
Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table...
. The electronic configuration of Si is
. We need consider only the outer electrons, for which it can be shown (see term symbols) that the possible terms allowed by the Pauli exclusion principlePauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
are
. Hund's first rule now states that the ground state term is which has . The superscript 3 is the value of the multiplicity = 2S + 1 = 3. The diagram shows the state of this term with ML = 1 and MS = 1.Rule #2
This rule deals again with reducing the repulsion between electrons. It can be understood from the classical picture that if all electrons are orbiting in the same direction (higher orbital angular momentum) they meet less often than if some of them orbit in opposite directions. In the latter case the repulsive force increases, which separates electrons. This adds potential energy to them, so their energy level is higher.Example
For silicon there is no choice of triplet stateTriplet state
A spin triplet is a set of three quantum states of a system, each with total spin S = 1 . The system could consist of a single elementary massive spin 1 particle such as a W or Z boson, or be some multiparticle state with total spin angular momentum of one.In physics, spin is the angular momentum...
s
, so the second rule is not required. The lightest atom which requires the second rule to determine the ground state is titaniumTitanium
Titanium is a chemical element with the symbol Ti and atomic number 22. It has a low density and is a strong, lustrous, corrosion-resistant transition metal with a silver color....
(Ti, Z = 22) with electron configuration 1s2 2s2 2p6 3s2 3p6 4s2 3d2. Following the same method as for Si, the allowed terms include three singlets (1S, 1D, and 1G)
and two triplets (3P and 3F). We deduce from Hund's first rule that the ground state is one of the two triplets, and from Hund's second rule that the ground state is 3F (with L = 3) rather than 3P (with L = 1). There is no
3G term since its (ML = 4, MS = 1) state would require two electrons each with (ML = 2, MS = +1/2), in violation of the Pauli principle.
Rule #3
This rule considers the energy shifts due to spin-orbit coupling. In the case where the spin-orbit coupling is weak compared to the residual electrostatic interaction, and are still good quantum numbers and the splitting is given by:The value of
changes from plus to minus for shells greater than half full. This term gives the dependence of the ground state energy on the magnitude of .Examples
The lowest energy term of Si consists of three levels, . With only two of six possible electrons in the shell, it is less than half-full and thus is the ground state.For sulfur
Sulfur
Sulfur or sulphur is the chemical element with atomic number 16. In the periodic table it is represented by the symbol S. It is an abundant, multivalent non-metal. Under normal conditions, sulfur atoms form cyclic octatomic molecules with chemical formula S8. Elemental sulfur is a bright yellow...
(S) the lowest energy term is again
with spin-orbit levels , but now there are four of six possible electrons in the shell so the ground state is .If the shell is half-filled then
, and hence there is only one value of (equal to ) which will be the lowest energy state. For example in phosphorusPhosphorus
Phosphorus is the chemical element that has the symbol P and atomic number 15. A multivalent nonmetal of the nitrogen group, phosphorus as a mineral is almost always present in its maximally oxidized state, as inorganic phosphate rocks...
the lowest energy state has
for three unpaired electrons in three 2p orbitals. Therefore and the ground state is 4S3/2.Excited states
Hund's rules work best for the determination of the ground stateGround state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
of an atom or molecule.
They are also fairly reliable (with occasional failures) for the determination of the lowest state of a given excited electronic configuration. Thus in the helium atom, the 1s2s triplet state (3S) is correctly predicted by Hund's first rule to be lower than the 1s2s singlet (1S). Similarly for organic molecules, the same rule predicts that the first triplet state (denoted by T1 in photochemistry
Photochemistry
Photochemistry, a sub-discipline of chemistry, is the study of chemical reactions that proceed with the absorption of light by atoms or molecules.. Everyday examples include photosynthesis, the degradation of plastics and the formation of vitamin D with sunlight.-Principles:Light is a type of...
) is lower than the first excited singlet state (S1), which is generally correct.
However Hund's rules should not be used to order states other than the lowest for a given configuration. For example, the titanium
Titanium
Titanium is a chemical element with the symbol Ti and atomic number 22. It has a low density and is a strong, lustrous, corrosion-resistant transition metal with a silver color....
atom ground state configuration is ...3d2 for which a naïve application of Hund's rules would suggest the ordering 3F < 3P < 1G < 1D < 1S. In reality, however, 1D lies below 1G.
See also
- Friedrich HundFriedrich HundFriedrich Hermann Hund was a German physicist from Karlsruhe known for his work on atoms and molecules.Hund worked at the Universities of Rostock, Leipzig, Jena, Frankfurt am Main, and Göttingen....
- Hund's rule of maximum multiplicityHund's rule of Maximum MultiplicityHund's Rule of Maximum Multiplicity is an observational rule which states that a greater total spin state usually makes the resulting atom more stable. Accordingly, it can be taken that if two or more orbitals of equal energy are available, electrons will occupy them singly before filling them in...
For the notation of orbital angular momentum L see: Spectroscopic notation
Spectroscopic notation
Spectroscopic notation provides various ways to specify atomic ionization states, as well as atomic and molecular orbitals.-Ionization states:Spectroscopists customarily refer to the spectrum arising from a given ionization state of a given element by the element's symbol followed by a Roman numeral...