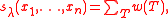Lindström–Gessel–Viennot lemma
Encyclopedia
In mathematics, the Lindström–Gessel–Viennot lemma provides a way to count the number of tuples of non-intersecting lattice paths.
. This means that each vertex has finite degree
, and that G contains no directed cycles. Consider base vertices
and destination vertices 
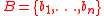, and also assign edge weights 
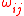for each directed edge. For each directed path P between two vertices, assign the corresponding formal product 
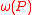of the edges of the path. For any two vertices a and b, write e(a,b) as the formal sum over all paths 
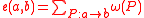. In particular, if between any two points there are only finitely many paths, one can assign the weight 1 to each edge and then e(a,b) counts the number of paths from a to b.
With this setup, write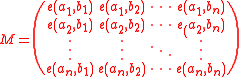
.
The Lindström–Gessel–Viennot lemma then states that the determinant of M is the signed sum over all n-tuples P = (P1, ..., Pn) of non-intersecting paths from A to B:
That is, the determinant of M counts the weights of all n-tuples of non-intersecting paths starting at A and ending at B, each affected with the sign of the corresponding permutation of
, given by 
taking 
to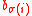 
.
In particular, if we can take the weights to be 1 and the only permutation possible is the identity (i.e., every n-tuple of non-intersecting paths from A to B takes ai to bi for each i), then det(M) is exactly the number of non-intersecting n-tuples of paths starting at A and ending at B.
s. Given a partition
of n, the Schur polynomial 
can be defined as:
where the sum is over all semistandard Young tableaux T of shape λ, and the weight of a tableau is given by the corresponding monomial, obtained by taking the product of the xi indexed by the entries of T. For instance, the weight of the tableau
is
.
where hi are the complete homogeneous symmetric polynomial
s. For instance, for the partition (3,2,2,1), the corresponding determinant is
To prove the equivalence, given any partition λ as above, with conjugate partition
, one considers the r starting points 
and the r ending points 
, as points in the lattice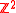 
, which acquires the structure of a directed graph by asserting that the only allowed directions are going one to the right or one up; the weight associated to any horizontal edge at height i is xi, and the weight associated to a vertical edge is 1. With this definition, r-tuples of paths from A to B are exactly semistandard Young tableaux of shape λ, and the weight of such an r-tuple is the corresponding summand in the first definition of the Schur polynomials. For instance, with the tableau
,
one gets the corresponding 4-tuple
On the other hand, the matrix M is exactly the matrix written above for D. This shows the required equivalence.
Statement
Let G be a locally finite directed acyclic graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. This means that each vertex has finite degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
, and that G contains no directed cycles. Consider base vertices
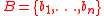and destination vertices , and also assign edge weights 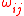for each directed edge. For each directed path P between two vertices, assign the corresponding formal product 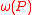of the edges of the path. For any two vertices a and b, write e(a,b) as the formal sum over all paths 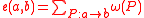. In particular, if between any two points there are only finitely many paths, one can assign the weight 1 to each edge and then e(a,b) counts the number of paths from a to b.With this setup, write
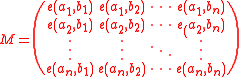.The Lindström–Gessel–Viennot lemma then states that the determinant of M is the signed sum over all n-tuples P = (P1, ..., Pn) of non-intersecting paths from A to B:
That is, the determinant of M counts the weights of all n-tuples of non-intersecting paths starting at A and ending at B, each affected with the sign of the corresponding permutation of
, given by 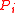taking 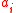to 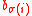.In particular, if we can take the weights to be 1 and the only permutation possible is the identity (i.e., every n-tuple of non-intersecting paths from A to B takes ai to bi for each i), then det(M) is exactly the number of non-intersecting n-tuples of paths starting at A and ending at B.
Proof
To prove the Lindström–Gessel–Viennot lemma, one uses an involution, whose fixed points are precisely the tuples of nonintersecting paths, and which preserves the weights. To define this involution f on the set of all n-tuples of paths from A to B, we define f to fix any tuple of nonintersecting paths, and for a tuple which contains an intersection, we want to switch the tails of the paths so as to give the negative sign in the above formula. To make sure this is well defined, it is necessary to define an ordering on the paths that intersect. Let i be the smallest index such that the path starting at ai contains an intersection, and then let j be the largest index such that a path intersecting the previous one starts at aj. Then define f to switch the tails of these two paths. This is a well defined involution on the set of all n-tuples of paths from A to B, whose fixed points is exactly the set of non-intersecting tuples.Schur polynomials
The Lindström–Gessel–Viennot lemma can be used to prove the equivalence of the following two different definitions of Schur polynomialSchur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
s. Given a partition
of n, the Schur polynomial can be defined as:
where the sum is over all semistandard Young tableaux T of shape λ, and the weight of a tableau is given by the corresponding monomial, obtained by taking the product of the xi indexed by the entries of T. For instance, the weight of the tableau
is
.
where hi are the complete homogeneous symmetric polynomial
Complete homogeneous symmetric polynomial
In mathematics, specifically in algebraic combinatorics and commutative algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials...
s. For instance, for the partition (3,2,2,1), the corresponding determinant is
To prove the equivalence, given any partition λ as above, with conjugate partition
, one considers the r starting points and the r ending points , as points in the lattice 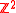, which acquires the structure of a directed graph by asserting that the only allowed directions are going one to the right or one up; the weight associated to any horizontal edge at height i is xi, and the weight associated to a vertical edge is 1. With this definition, r-tuples of paths from A to B are exactly semistandard Young tableaux of shape λ, and the weight of such an r-tuple is the corresponding summand in the first definition of the Schur polynomials. For instance, with the tableau,
one gets the corresponding 4-tuple
On the other hand, the matrix M is exactly the matrix written above for D. This shows the required equivalence.