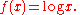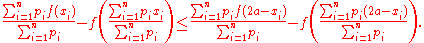Levinson's inequality
Encyclopedia
In mathematics
, Levinson's inequality is the following inequality, due to Norman Levinson
, involving positive numbers. Let and let
and let  be a given function having a third derivative on the range
be a given function having a third derivative on the range 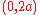 , and such that
, and such that
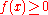
for all . Suppose
. Suppose 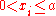 for
for  and
and  . Then
. Then
The Ky Fan inequality
is the special case of Levinson's inequality where

and
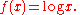
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Levinson's inequality is the following inequality, due to Norman Levinson
Norman Levinson
Norman Levinson was an American mathematician. Some of his major contributions were in the study of Fourier transforms, complex analysis, non-linear differential equations, number theory, and signal processing. He worked closely with Norbert Wiener in his early career...
, involving positive numbers. Let
 and let
and let  be a given function having a third derivative on the range
be a given function having a third derivative on the range 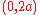 , and such that
, and such that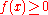
for all
 . Suppose
. Suppose 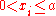 for
for  and
and  . Then
. ThenThe Ky Fan inequality
Ky Fan inequality
In mathematics, there are two different results that share the common name of the Ky Fan inequality. One is an inequality involving the geometric mean and arithmetic mean of two sets of real numbers of the unit interval. The result was published on page 5 of the book Inequalities by...
is the special case of Levinson's inequality where

and