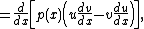Lagrange's identity (boundary value problem)
Encyclopedia
In the study of ordinary differential equation
s and their associated boundary value problem
s, Lagrange's identity, named after Joseph Louis Lagrange
, gives the boundary terms arising from integration by parts
of a self-adjoint linear differential operator
. Lagrange's identity is fundamental in Sturm–Liouville theory. In more than one independent variable, Lagrange's identity is generalized by Green's second identity.
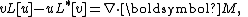
where:
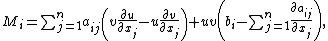
and
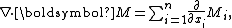
The operator L and its adjoint operator L* are given by:
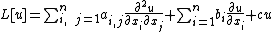
and
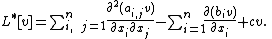
If Lagrange's identity is integrated over a bounded region, then the divergence theorem
can be used to form Green's second identity in the form:
where S is the surface bounding the volume Ω and n is the unit outward normal to the surface S.
of the form:
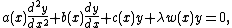
can be put in the form:
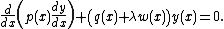
This general form motivates introduction of the Sturm–Liouville operator L, defined as an operation upon a function f such that:
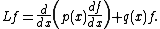
It can be shown that for any u and v for which the various derivatives exist, Lagrange's identity for ordinary differential equations holds:
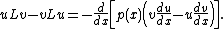
For ordinary differential equations defined in the interval [0, 1], Lagrange's identity can be integrated to obtain an integral form (also known as Green's formula):
where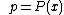
, 
, 
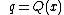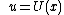and 
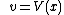are functions of 
. 
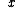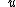and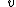 
having continuous second derivatives on the
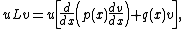
and
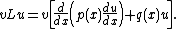
Subtracting:
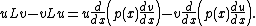
The leading multiplied u and v can be moved inside the differentiation, because the extra differentiated terms in u and v are the same in the two subtracted terms and simply cancel each other. Thus,
which is Lagrange's identity. Integrating from zero to one:
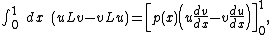
as was to be shown.
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s and their associated boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s, Lagrange's identity, named after Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, gives the boundary terms arising from integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
of a self-adjoint linear differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
. Lagrange's identity is fundamental in Sturm–Liouville theory. In more than one independent variable, Lagrange's identity is generalized by Green's second identity.
Statement
In general terms, Lagrange's identity for any pair of functions u and v in function space C2 (that is, twice differentiable) in n dimensions is: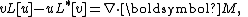where:
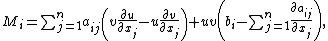
and
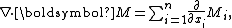
The operator L and its adjoint operator L* are given by:
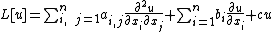
and
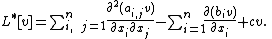
If Lagrange's identity is integrated over a bounded region, then the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
can be used to form Green's second identity in the form:
where S is the surface bounding the volume Ω and n is the unit outward normal to the surface S.
Ordinary differential equations
Any second order ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
of the form:
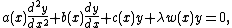
can be put in the form:
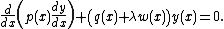
This general form motivates introduction of the Sturm–Liouville operator L, defined as an operation upon a function f such that:
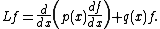
It can be shown that for any u and v for which the various derivatives exist, Lagrange's identity for ordinary differential equations holds:
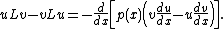
For ordinary differential equations defined in the interval [0, 1], Lagrange's identity can be integrated to obtain an integral form (also known as Green's formula):
where
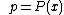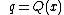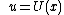, , and 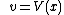are functions of 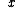. 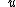and 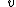having continuous second derivatives on the Proof of form for ordinary differential equations
We have: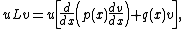and
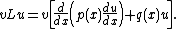
Subtracting:
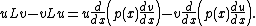
The leading multiplied u and v can be moved inside the differentiation, because the extra differentiated terms in u and v are the same in the two subtracted terms and simply cancel each other. Thus,
which is Lagrange's identity. Integrating from zero to one:
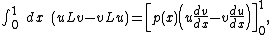
as was to be shown.