Kirkman's schoolgirl problem
Encyclopedia
Kirkman's schoolgirl problem is a problem in combinatorics
proposed by Thomas Kirkman in 1850 as Query VI in The Lady's and Gentleman's Diary. The problem states:
A solution to this problem is an example of a Kirkman triple system, which is a Steiner triple system having a parallelism, that is, a partition of the blocks of the triple system into parallel classes which are themselves partitions of the points into disjoint blocks.
There are seven non-isomorphic solutions to the schoolgirl problem. Two of these are packings of the finite projective space
PG(3,2). A packing of a projective space is a partition of the lines of the space into spreads, and a spread is a partition of the points of the space into lines.
girls, where 
must be an odd multiple of 3, walking in triplets for
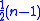
days, with the requirement, again, that no pair of girls walk in the same row twice. The solution to this generalisation is a Steiner triple system
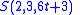
with parallelism (that is, one in which each of the 6t + 3 elements occurs exactly once in each block of 3-element sets), known as a Kirkman triple system. It is this generalization of the problem that Kirkman discussed first, while the famous special case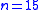
was only proposed later. A complete solution to the general case was given by D. K. Ray-Chaudhuri
and R. M. Wilson
in 1969.
Many variations of the basic problem can be considered. Alan Hartman solves a problem of this type with the requirement that no trio walks in a row of four more than once using Steiner quadruple systems.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
proposed by Thomas Kirkman in 1850 as Query VI in The Lady's and Gentleman's Diary. The problem states:
Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily so that no two shall walk twice abreast.
Solution
If the girls are numbered from 01 to 15, the following arrangement is one solution:| Sun. | Mon. | Tues. | Wed. | Thurs. | Fri. | Sat. |
|---|---|---|---|---|---|---|
| 01, 06, 11 | 01, 02, 05 | 02, 03, 06 | 05, 06, 09 | 03, 05, 11 | 05, 07, 13 | 11, 13, 04 |
| 02, 07, 12 | 03, 04, 07 | 04, 05, 08 | 07, 08, 11 | 04, 06, 12 | 06, 08, 14 | 12, 14, 05 |
| 03, 08, 13 | 08, 09, 12 | 09, 10, 13 | 12, 13, 01 | 07, 09, 15 | 09, 11, 02 | 15, 02, 08 |
| 04, 09, 14 | 10, 11, 14 | 11, 12, 15 | 14, 15, 03 | 08, 10, 01 | 10, 12, 03 | 01, 03, 09 |
| 05, 10, 15 | 13, 15, 06 | 14, 01, 07 | 02, 04, 10 | 13, 14, 02 | 15, 01, 04 | 06, 07, 10 |
A solution to this problem is an example of a Kirkman triple system, which is a Steiner triple system having a parallelism, that is, a partition of the blocks of the triple system into parallel classes which are themselves partitions of the points into disjoint blocks.
There are seven non-isomorphic solutions to the schoolgirl problem. Two of these are packings of the finite projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
PG(3,2). A packing of a projective space is a partition of the lines of the space into spreads, and a spread is a partition of the points of the space into lines.
Generalization
The problem can be generalized to girls, where must be an odd multiple of 3, walking in triplets for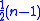days, with the requirement, again, that no pair of girls walk in the same row twice. The solution to this generalisation is a Steiner triple system
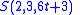
with parallelism (that is, one in which each of the 6t + 3 elements occurs exactly once in each block of 3-element sets), known as a Kirkman triple system. It is this generalization of the problem that Kirkman discussed first, while the famous special case
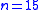was only proposed later. A complete solution to the general case was given by D. K. Ray-ChaudhuriD. K. Ray-Chaudhuri
Dwijendra Kumar Ray-Chaudhuri a Bengali Indian born mathematician and a statistician is a professor emeritusat Ohio State University. He and his student R. M...
and R. M. Wilson
R. M. Wilson
Richard Michael Wilson is a mathematician and a professor at the California Institute of Technology. Wilson and D. K. Ray-Chaudhuri, , solved Kirkman's schoolgirl problem in 1968. Wilson is known for his work in combinatorial mathematics.-References:*...
in 1969.
Many variations of the basic problem can be considered. Alan Hartman solves a problem of this type with the requirement that no trio walks in a row of four more than once using Steiner quadruple systems.