Kingman's formula
Encyclopedia
In queueing theory
, Kingman's formula is an approximation for G/G/1
queues and states that the mean waiting time is given by
Where
is the mean service time (i.e. 
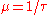is the service rate), 
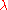is the mean arrival rate, 
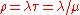is the utilization, ca is the coefficient of variation
for arrivals (that is the standard deviation of arrival times divided by the mean arrival time) and cs is the coefficient of variation for service times (standard deviation of service time divided by mean service time
).
The formula is the product of three terms, which depend on Utilization, Variability and Service time, respectively. This has a nice interpretation: it shows that the expected waiting time increases when service is slow, or when service and/or arrival times are highly variable or when the system is very busy (rho close to one).
It was first published by John Kingman
in his 1966 paper "On the Algebra of Queues." It is known to be generally very accurate for a system that is operating close to saturation.
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, Kingman's formula is an approximation for G/G/1
Kendall's notation
In queueing theory, Kendall's notation is the standard system used to describe and classify the queueing model that a queueing system corresponds to. First suggested by D. G...
queues and states that the mean waiting time is given by
Where
is the mean service time (i.e. 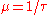is the service rate), 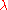is the mean arrival rate, 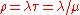is the utilization, ca is the coefficient of variationCoefficient of variation
In probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
for arrivals (that is the standard deviation of arrival times divided by the mean arrival time) and cs is the coefficient of variation for service times (standard deviation of service time divided by mean service time
).The formula is the product of three terms, which depend on Utilization, Variability and Service time, respectively. This has a nice interpretation: it shows that the expected waiting time increases when service is slow, or when service and/or arrival times are highly variable or when the system is very busy (rho close to one).
It was first published by John Kingman
John Kingman
Sir John Frank Charles Kingman, born on 28 August 1939 in Beckenham, Kent, is a British mathematician.He was N. M. Rothschild and Sons Professor of Mathematical Sciences and Director of the Isaac Newton Institute at the University of Cambridge from 2001 until 2006, when he was succeeded by Sir...
in his 1966 paper "On the Algebra of Queues." It is known to be generally very accurate for a system that is operating close to saturation.