Hoeffding's inequality
Encyclopedia
In probability theory
, Hoeffding's inequality provides an upper bound
on the probability
for the sum of random variables to deviate from its expected value
. Hoeffding's inequality was proved by Wassily Hoeffding
.
Let
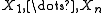
be independent random variables. Assume that the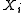
are almost surely bounded; that is, assume for 
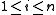that
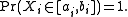
Then, for the empirical mean of these variables
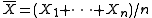
we have the inequalities (Hoeffding 1963, Theorem 2 ):
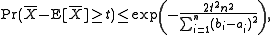
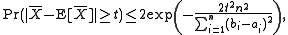
which are valid for positive values of t. Here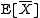
is the expected value
of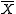
.
These inequalities are special cases of the more general Azuma–Hoeffding inequality and the even more general Bernstein inequality in probability theory, proved by Sergei Bernstein in 1923. They are also special cases of McDiarmid's inequality.
Note that the inequalities also hold when the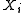
have been obtained using sampling without replacement; in this case the random variables are not independent anymore. A proof of this statement can be found in Hoeffding's paper. For slightly better bounds in the case of sampling without replacement, see for instance the paper by Serfling .
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Hoeffding's inequality provides an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
on the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
for the sum of random variables to deviate from its expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. Hoeffding's inequality was proved by Wassily Hoeffding
Wassily Hoeffding
Wassily Hoeffding was an American statistician and probabilist...
.
Let
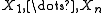
be independent random variables. Assume that the
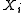are almost surely bounded; that is, assume for 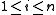that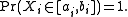Then, for the empirical mean of these variables
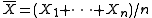
we have the inequalities (Hoeffding 1963, Theorem 2 ):
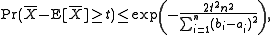
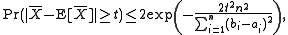
which are valid for positive values of t. Here
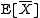is the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of
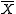.These inequalities are special cases of the more general Azuma–Hoeffding inequality and the even more general Bernstein inequality in probability theory, proved by Sergei Bernstein in 1923. They are also special cases of McDiarmid's inequality.
Note that the inequalities also hold when the
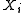have been obtained using sampling without replacement; in this case the random variables are not independent anymore. A proof of this statement can be found in Hoeffding's paper. For slightly better bounds in the case of sampling without replacement, see for instance the paper by Serfling .See also
- Bennett's inequalityBennett's inequalityIn probability theory, Bennett's inequality provides an upper bound on the probability that the sum of independent random variables deviates from its expected value by more than any specified amount...
- Chebyshev's inequalityChebyshev's inequalityIn probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
- Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
- Chernoff bounds
- Hoeffding's lemmaHoeffding's lemmaIn probability theory, Hoeffding's lemma is an inequality that bounds the moment-generating function of any bounded random variable. It is named after the Finnish–American mathematical statistician Wassily Hoeffding....