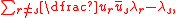Hilbert's inequality
Encyclopedia
In complex analysis
, a branch of mathematics, Hilbert's inequality was first demonstrated by David Hilbert
and later improved by Issai Schur
, who replaced Hilbert's constant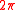 with the sharp constant
with the sharp constant  .
.
Let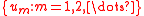 be complex numbers, Hilbert's inequality is
be complex numbers, Hilbert's inequality is
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics, Hilbert's inequality was first demonstrated by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
and later improved by Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
, who replaced Hilbert's constant
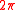 with the sharp constant
with the sharp constant  .
.Let
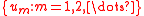 be complex numbers, Hilbert's inequality is
be complex numbers, Hilbert's inequality is-
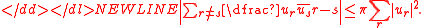
In 1973, Montgomery & Vaughan reported several generalizations of Hilbert's inequality, considering the bilinear forms
and
where are distinct real numbers modulo 1 (i.e. they belong to distinct classes in the quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
are distinct real numbers modulo 1 (i.e. they belong to distinct classes in the quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
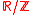 ) and
) and 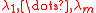 are distinct real numbers. Montgomery & Vaughan's generalizations of Hilbert's inequality are then given by
are distinct real numbers. Montgomery & Vaughan's generalizations of Hilbert's inequality are then given by
-

and
-

where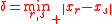 and
and 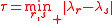 (where
(where 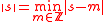 is the distance from
is the distance from  to the nearest integer and
to the nearest integer and  denotes the smallest positive value). Moreover, if
denotes the smallest positive value). Moreover, if 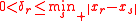 and
and 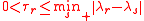 then the following inequalities holds:
then the following inequalities holds:
-

and
-
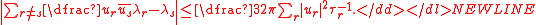
In their paper they give conditions by which the above sums are allowed to be infinite sum.
See also
- Hugh Montgomery (mathematician)
- David HilbertDavid HilbertDavid Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
- Online book chapter Hilbert’s Inequality and Compensating Difficulties extracted from .
-
-
-
-