
Herbrand's theorem (proof theory)
Encyclopedia
Herbrand's theorem is a fundamental result of mathematical logic
obtained by Jacques Herbrand
(1930). It essentially allows a certain kind of reduction of first-order logic
to propositional logic. Although Herbrand originally proved his theorem for arbitrary formulas of first-order logic, the simpler version shown here, restricted to formulas in prenex form containing only existential quantifiers became more popular.
Let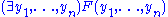
be a formula of first-order logic with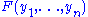 quantifier-free.
quantifier-free.
Then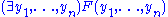
is valid if and only if there exists a finite sequence of terms: , with
, with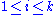 and
and 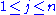 ,
,
such that
is valid. If it is valid,
is called a Herbrand disjunction for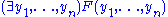 .
.
Informally: a formula in prenex form containing existential quantifiers only is provable (valid) in first-order logic if and only if a disjunction composed of substitution instances of the quantifier-free subformula of
in prenex form containing existential quantifiers only is provable (valid) in first-order logic if and only if a disjunction composed of substitution instances of the quantifier-free subformula of 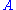 is a tautology
is a tautology
(propositionally derivable).
The restriction to formulas in prenex form containing only existential quantifiers does not limit the generality of the theorem, because formulas can be converted to prenex form and their universal quantifiers can be removed by Herbrandization
. Conversion to prenex form can be avoided, if structural Herbrandization is performed. Herbrandization can be avoided by imposing additional restrictions on the variable dependencies allowed in the Herbrand disjunction.
However, sequent calculus
and cut-elimination were not known at the time of Herbrand's theorem, and Herbrand had to prove his theorem in a more complicated way.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
obtained by Jacques Herbrand
Jacques Herbrand
Jacques Herbrand was a French mathematician who was born in Paris, France and died in La Bérarde, Isère, France. Although he died at only 23 years of age, he was already considered one of "the greatest mathematicians of the younger generation" by his professors Helmut Hasse, and Richard Courant.He...
(1930). It essentially allows a certain kind of reduction of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
to propositional logic. Although Herbrand originally proved his theorem for arbitrary formulas of first-order logic, the simpler version shown here, restricted to formulas in prenex form containing only existential quantifiers became more popular.
Let
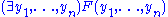
be a formula of first-order logic with
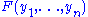 quantifier-free.
quantifier-free.Then
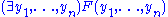
is valid if and only if there exists a finite sequence of terms:
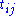 , with
, with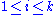 and
and 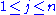 ,
,such that

is valid. If it is valid,

is called a Herbrand disjunction for
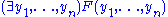 .
.Informally: a formula
 in prenex form containing existential quantifiers only is provable (valid) in first-order logic if and only if a disjunction composed of substitution instances of the quantifier-free subformula of
in prenex form containing existential quantifiers only is provable (valid) in first-order logic if and only if a disjunction composed of substitution instances of the quantifier-free subformula of 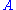 is a tautology
is a tautologyTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
(propositionally derivable).
The restriction to formulas in prenex form containing only existential quantifiers does not limit the generality of the theorem, because formulas can be converted to prenex form and their universal quantifiers can be removed by Herbrandization
Herbrandization
The Herbrandization of a logical formula is a construction that is dual to the Skolemization of a formula. Thoralf Skolem had considered the Skolemizations of formulas in prenex form as part of his proof of the Löwenheim-Skolem theorem...
. Conversion to prenex form can be avoided, if structural Herbrandization is performed. Herbrandization can be avoided by imposing additional restrictions on the variable dependencies allowed in the Herbrand disjunction.
Proof Sketch
A proof of the non-trivial direction of the theorem can be constructed according to the following steps:- If the formula
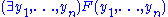 is valid, then by completeness of cut-free sequent calculusSequent calculusIn proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
is valid, then by completeness of cut-free sequent calculusSequent calculusIn proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, which follows from Gentzen's cut-elimination theorem, there is a cut-free proof of .
. - Starting from above downwards, remove the inferences that introduce existential quantifiers.
- Remove contraction-inferences on previously existentially quantified formulas, since the formulas (now with terms substituted for previously quantified variables) might not be identical anymore after the removal of the quantifier inferences.
- The removal of contractions accumulates all the relevant substitution instances of
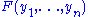 in the right side of the sequent, thus resulting in a proof of
in the right side of the sequent, thus resulting in a proof of  , from which the Herbrand disjunction can be obtained.
, from which the Herbrand disjunction can be obtained.
However, sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
and cut-elimination were not known at the time of Herbrand's theorem, and Herbrand had to prove his theorem in a more complicated way.
Generalizations of Herbrand's Theorem
- Herbrand's theorem has been extended to arbitrary higher-order logics by using expansion-tree proofs. The deep representation of expansion-tree proofs correspond to Herbrand disjunctions, when restricted to first-order logic.
- Herbrand disjunctions and expansion-tree proofs have been extended with a notion of cut. Due to the complexity of cut-elimination, herbrand disjunctions with cuts can be non-elementarily smaller than a standard herbrand disjunction.
- Herbrand disjunctions have been generalized to Herbrand sequents, allowing Herbrand's theorem to be stated for sequents: "a skolemized sequent is derivable iff it has a Herbrand sequent".
See also
- Herbrand structure,
- Herbrand interpretationHerbrand interpretationIn mathematical logic, a Herbrand interpretation is an interpretation in which all constants and function symbols are assigned very simple meanings. Specifically, every constant is interpreted as itself, and every function symbol is interpreted as the function that applies it...
- Herbrand universe
- Compactness theoremCompactness theoremIn mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...

