
Hadamard's lemma
Encyclopedia
In mathematics
, Hadamard's lemma, named after Jacques Hadamard
, is essentially a first-order form of Taylor's theorem
, in which we can express a smooth, real-valued function exactly in a convenient manner.

where each gi is a smooth function on U, a = (a1,...,an), and x = (x1,...,xn).
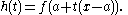
Then since
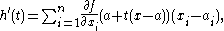
we have
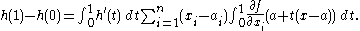
But additionally, h(1) − h(0) = f(x) − f(a), so if we let
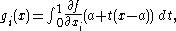
we have proven the theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hadamard's lemma, named after Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
, is essentially a first-order form of Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
, in which we can express a smooth, real-valued function exactly in a convenient manner.
Statement
Let ƒ be a smooth, real-valued function defined on an open, star-convex neighborhood U of a point a in n-dimensional Euclidean space. Then ƒ(x) can be expressed, for all x in U, in the form:
where each gi is a smooth function on U, a = (a1,...,an), and x = (x1,...,xn).
Proof
Let x be in U. Let h be the map from [0,1] to the real numbers defined by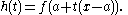
Then since
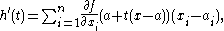
we have
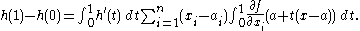
But additionally, h(1) − h(0) = f(x) − f(a), so if we let
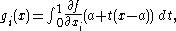
we have proven the theorem.

