Gentzen's consistency proof
Encyclopedia
Gentzen's consistency proof is a result of proof theory
in mathematical logic
. It "reduces" the consistency of a simplified part of mathematics, not to something that could be proved (which would contradict the basic results of Kurt Gödel
), but to clarified logical principles.
proved the consistency of first-order arithmetic using combinatorial methods. Gentzen's proof shows much more than merely that first-order arithmetic is consistent. Gentzen showed that the consistency of first-order arithmetic is provable, over the base theory of primitive recursive arithmetic
with the additional principle of quantifier free transfinite induction
up to the ordinal
ε0 (epsilon nought
). Informally, this additional principle means that there is a well-ordering on the set of finite rooted trees.
The principle of quantifier free transfinite induction up to ε0 says that for any formula A(x) with no bound variables transfinite induction up to ε0 holds. ε0 is the first ordinal
, such that 
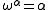, i.e. the limit of the sequence:
To express ordinals in the language of arithmetic an ordinal notation
is needed, i.e. a way to assign natural numbers to ordinals less than ε0. This can be done in various ways, one example provided by Cantor's normal form theorem. That transfinite induction holds for a formula A(x) means that A does not define an infinite descending sequence of ordinals smaller than ε0 (in which case ε0 would not be well-ordered). Gentzen assigned ordinals smaller than ε0 to proofs in first-order arithmetic and showed that if there is a proof of contradiction, then there is an infinite descending sequence of ordinals < ε0 produced by a primitive recursive operation on proofs corresponding to a quantifier free formula.
Gentzen's proof is the first example of what is called proof theoretical ordinal analysis
. In ordinal analysis one gauges the strength of theories by measuring how large the (constructive) ordinals are that can be proven to be well-ordered, or equivalently for how large a (constructive) ordinal can transfinite induction be proven. A constructive ordinal is the order type of a recursive
well-ordering of natural numbers.
Laurence Kirby and Jeff Paris
proved in 1982 that Goodstein's theorem
cannot be proven in Peano arithmetic based on Gentzen's theorem.
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
. It "reduces" the consistency of a simplified part of mathematics, not to something that could be proved (which would contradict the basic results of Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
), but to clarified logical principles.
Gentzen's theorem
In 1936 Gerhard GentzenGerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
proved the consistency of first-order arithmetic using combinatorial methods. Gentzen's proof shows much more than merely that first-order arithmetic is consistent. Gentzen showed that the consistency of first-order arithmetic is provable, over the base theory of primitive recursive arithmetic
Primitive recursive arithmetic
Primitive recursive arithmetic, or PRA, is a quantifier-free formalization of the natural numbers. It was first proposed by Skolem as a formalization of his finitist conception of the foundations of arithmetic, and it is widely agreed that all reasoning of PRA is finitist...
with the additional principle of quantifier free transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
up to the ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
ε0 (epsilon nought
Epsilon nought
In mathematics, the epsilon numbers are a collection of transfinite numbers whose defining property is that they are fixed points of an exponential map. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like...
). Informally, this additional principle means that there is a well-ordering on the set of finite rooted trees.
The principle of quantifier free transfinite induction up to ε0 says that for any formula A(x) with no bound variables transfinite induction up to ε0 holds. ε0 is the first ordinal
, such that 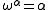, i.e. the limit of the sequence:To express ordinals in the language of arithmetic an ordinal notation
Ordinal notation
In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....
is needed, i.e. a way to assign natural numbers to ordinals less than ε0. This can be done in various ways, one example provided by Cantor's normal form theorem. That transfinite induction holds for a formula A(x) means that A does not define an infinite descending sequence of ordinals smaller than ε0 (in which case ε0 would not be well-ordered). Gentzen assigned ordinals smaller than ε0 to proofs in first-order arithmetic and showed that if there is a proof of contradiction, then there is an infinite descending sequence of ordinals < ε0 produced by a primitive recursive operation on proofs corresponding to a quantifier free formula.
Relation to Gödel's theorem
Gentzen's proof also highlights one commonly missed aspect of Gödel's second incompleteness theorem. It is sometimes claimed that the consistency of a theory can only be proved in a stronger theory. The theory obtained by adding quantifier free transfinite induction to primitive recursive arithmetic proves the consistency of first-order arithmetic but is not stronger than first-order arithmetic. For example, it does not prove ordinary mathematical induction for all formulae, while first-order arithmetic does (it has this as an axiom schema). The resulting theory is not weaker than first-order arithmetic either, since it can prove a number theoretical fact - the consistency of first-order arithmetic - that first-order arithmetic cannot. The two theories are simply incomparable.Gentzen's proof is the first example of what is called proof theoretical ordinal analysis
Ordinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
. In ordinal analysis one gauges the strength of theories by measuring how large the (constructive) ordinals are that can be proven to be well-ordered, or equivalently for how large a (constructive) ordinal can transfinite induction be proven. A constructive ordinal is the order type of a recursive
Recursive set
In computability theory, a set of natural numbers is called recursive, computable or decidable if there is an algorithm which terminates after a finite amount of time and correctly decides whether or not a given number belongs to the set....
well-ordering of natural numbers.
Laurence Kirby and Jeff Paris
Jeff Paris
Jeffrey Bruce Paris is a British mathematician known for his work on mathematical logic, in particular provability in arithmetic, uncertain reasoning and inductive logic with an emphasis on rationality and common sense principles....
proved in 1982 that Goodstein's theorem
Goodstein's theorem
In mathematical logic, Goodstein's theorem is a statement about the natural numbers, made by Reuben Goodstein, which states that every Goodstein sequence eventually terminates at 0. showed that it is unprovable in Peano arithmetic...
cannot be proven in Peano arithmetic based on Gentzen's theorem.